Optimizing Graph Coloring with Reinforcement Learning

Posted on January 6, 2025 by stefanutti

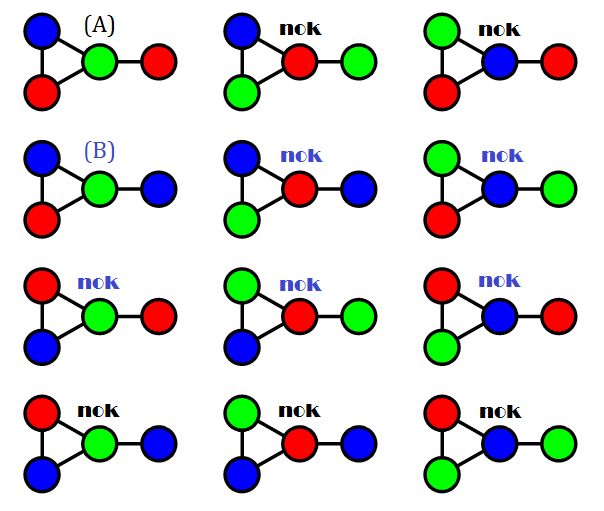
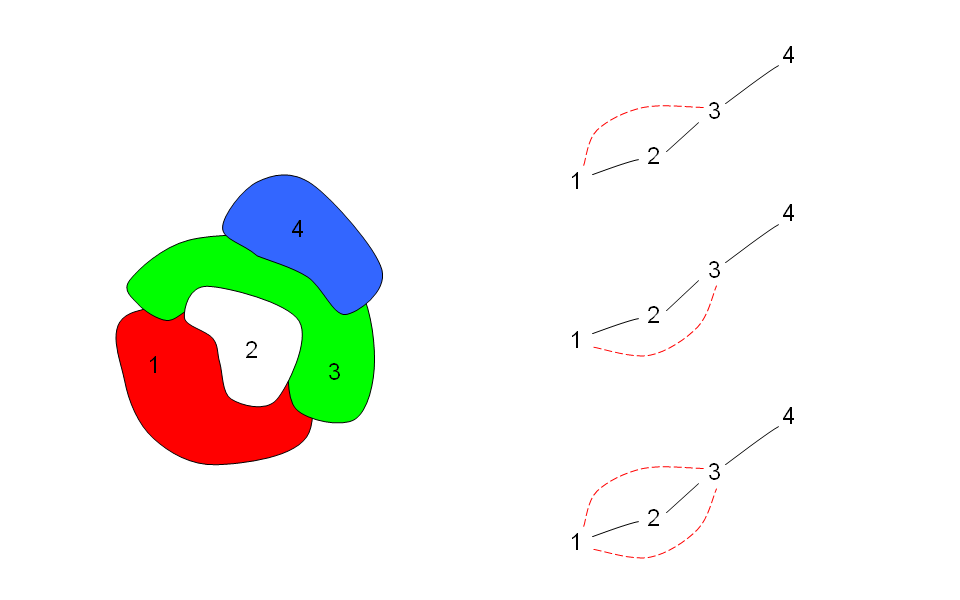
This is what I will be working for a while. Restart is difficult, but necessary.

Why use Reinforcement Learning for Graph coloring?

In my Python application, that works on 3-regular planar graph, deciding which is the order of the edges to remove can be non-trivial. A naive approach randomly picks edges from F2 faces, F3, F4 or F5. This is the approach I used :-(. It leads to impasses when rebuilding the map. See https://4coloring.wordpress.com/2014/08/27/four-color-theorem-experimenting-impasses-as-in-life/

But a reinforcement learning agent can learn to make better selections over time to reduce color conflicts, I hope :-), and shed light on some properties of the graph that can be used in the proof.

The code will be here: https://github.com/stefanutti/maps-coloring-python

Remove one edge at a time from F2, F3, F4, or F5 faces. These faces represent the basic unavoidable set. This process will reduce the map to three faces, including the ocean as the external area. Afterward, I will restore the edges in reverse order, consistently working with 3-regular planar graphs. I will consider Tait coloring of the edges and apply, when necessary, Kempe’s chain color switching to the edges.

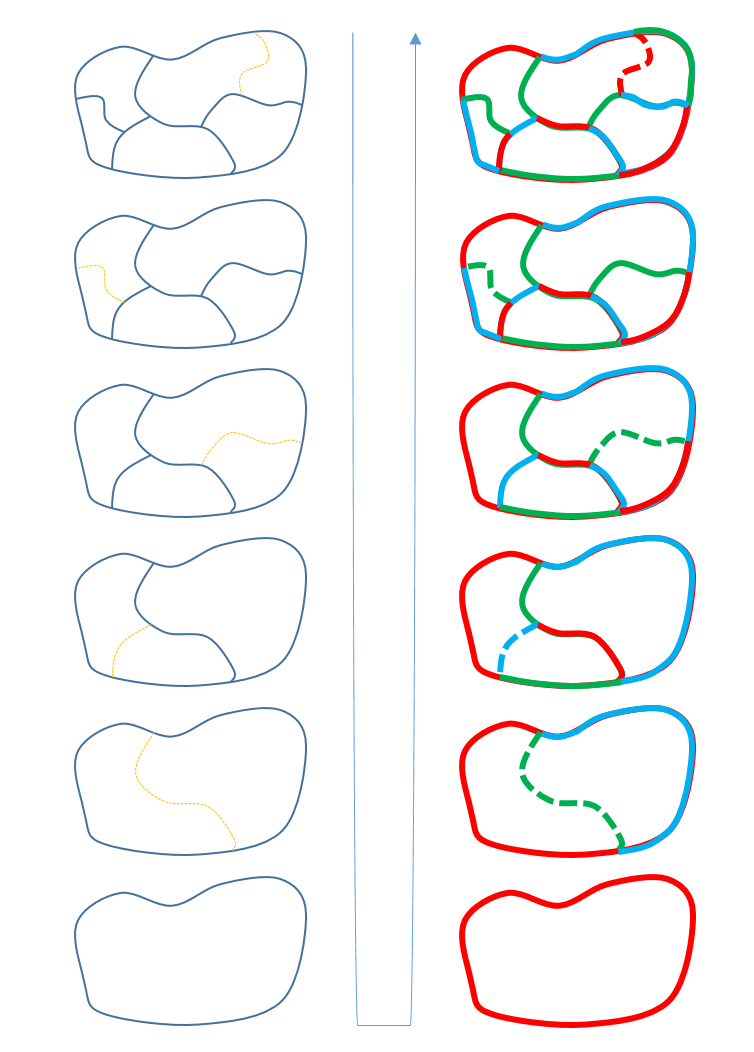
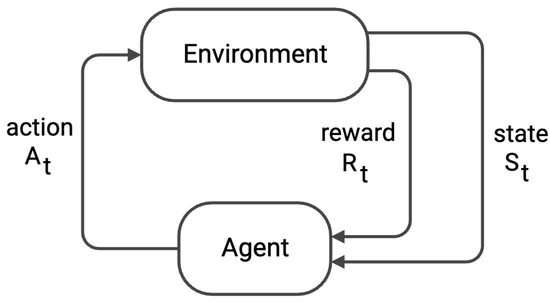
For the Agent:

Environment initialization = The starting uncolored 3-regular planar graphs
Action = Select the edge to remove from the 3-regular planar graphs
State = The updated 3-regular planar graphs
Reward = +1 if Random Kempe’s chain color switching was not necessary, -1 otherwise

Four color theorem: other representations of maps

Posted on May 19, 2011 by stefanutti

Here are some new representation of graphs:

Thanks to:

Four color theorem: representations of maps

Posted on April 25, 2011 by stefanutti

For the scope of the four color problem and without lack of generality, maps can be represented in different ways. This is generally done to have a different perspective on the problem.

For example, the graph-theoretic representation of maps has become so common and important that generally the four color problem is stated and analyzed directly in terms of graph theory: http://en.wikipedia.org/wiki/Four_color_theorem.

I am trying to collect other representations that may in some way help to get a different point of view on the problem. If you know one of these representations that is not listed and wish to share, report it here. If you also have a web reference that explains or shows the representation, it would be great.

The representations have to be general and applicable to all maps with the simplification that only regular maps (no exclaves or enclaves, 3 edges meeting at each vertex, etc.) can be considered.

These are some classic representations:

Natural: As a 3-regular planar graph (boundaries = edges)
Canonical: As the dual graph of the “natural” representation (region = vertex, neighbors = edges)
As a straight line drawing graph (Fáry’s theorem)
As a graph with vertices arranged on a grid
As a rectilinear cartogram

Plus, I found these:

As a circular map
As a rectangular map
As clefs (derived from rectangular maps)
As pipes map (derived from the clefs representation)
…

New representations (answers from mathoverflow):

http://en.wikipedia.org/wiki/Circle_packing_theorem (Koebe–Andreev–Thurston theorem)
As hypergraphs induced by discs (see: “ON THE CHROMATIC NUMBER OF GEOMETRIC HYPERGRAPHS” by SHAKHAR SMORODINSKY)

Here is an example of some of these representations for the original map shown:

See next post for other representations.

Counting maps

Posted on April 19, 2011 by stefanutti

I’ve posted this question on mathoverflow.

Is there a formula to count how many different topological regular maps can be created with n faces (on a sphere)?

For “regular” I intend maps in which the boundaries form a 3-regular planar graph
For “different” I intend maps that cannot be topologically transformed one into another (faces have to be considered unnamed)

I’ve been looking for a formula, but it is too difficult for me. Maybe it has a simple solution but I don’t see it.

This was my best guess, but I already know that it is not correct because full of symmetries, as it can be verified manually.

General formula:

$2\sum _{s_{(f-3)}=2f-5}^{2f-5+2} \text{...}\sum _{s_3=7}^{s_4} \sum _{s_2=5}^{s_3} \sum _{s_1=3}^{s_2} s_1\left(s_1-1\right)\left(s_2-3\right)\left(s_3-5\right)\text{...}\left(s_{(f-3)}-((2f-5)-2)\right)$

4 faces = $2\sum _{s_1=3}^5 s_1\left(s_1-1\right)$
5 faces = $2\sum _{s_2=5}^7 \sum _{s_1=3}^{s_2} s_1\left(s_1-1\right)\left(s_2-3\right)$

Here are the first results that can be found manually (excluding simmetrical maps):

2 faces = 0 possible regular map (an island and the ocean) (not to be counted, because not regular)
3 faces = 1 possible regular map (an island with two regions and the ocean) (two islands and the ocean wouldn’t be regular)
4 faces = 3 possible regular maps (can be verified adding a face from the previous map)
5 faces = 16 possible regular maps (with homeomorphics eliminated)
…

These are all maps up to 5 faces:

Four color theorem: recap

Posted on April 18, 2011 by stefanutti

Recap (some facts about maps and coloring):

All regular maps (3-regular planar graphs) can be topologically transformed (represented) as circular or rectangular maps
In searching for a solution of the four color problem, it is possible to exclude maps with faces that have less then five neighbours
Simplified maps (no faces with less than five neighbours) of 13 faces do not exist!
The nunber of proper colorings (not considering permulations of colors) can be count using the “Chromatic polynomial” and dividing the result by 4! (factorial that counts the permutations). Chromatic polynomial is only known for few types of graphs (Triangle K3, Complete graph Kn, Petersen graph, …)
Dual graphs derived from maps can be arranged with vertices positioned on a grid (see “Rectangular grid drawings of plane graphs” by Md. Saidur Rahman, Shin-ichi Nakano, Takao Nishizeki)
…

To implement on the Java application (https://github.com/stefanutti/maps-coloring-java):

Force faces to have fixed colors
Change swixml2 (http://code.google.com/p/swixml2) to swixml (https://github.com/swixml)
Change the graphic library G to JTS (https://www.vividsolutions.com/open-source)
…

Are these different colorings?

Posted on April 5, 2011 by stefanutti

UPDATE (18/Apr/2011)

The nunber of proper colorings (not considering permutations of colors) can be count using the “Chromatic polynomial” and dividing the result by 4! (factorial that counts the permutations). But, the chromatic polynomial is only known for few types of graphs (Triangle K3, Complete graph Kn, Petersen graph, …). I haven’t found papers on this problem. Highly propably, since the difficulty to find the Chromatic polynomial of complex graphs, there cannot be a direct formula to calculate how many different colorings exist.

I’ve posted this question here on mathoverflow.

END UPDATE

Take a look at these three graphs:

Are these really different colorings?

Before to dismiss this, do the following on the first graph:

Change Blue to Yellow (Blue was just an arbitrary color among infinite others)
Change Green to Blue
Change Yellow to Green

Now you have the second graph. Continue with this:

Change Green to Yellow
Change Red to Green
Change Yellow to Red

Now you have the third graph. Since the arbitrary nature of the choice of colors, the first graph could have been colored as the third one since the beginning.

The same result, can be obtained by changing all three colors of the first graph to three other colors. If applying the same method to the third graph, you can get the same configuration for the two graphs, it means that they can be considered, for some areas of investigation, as the same configuration.

There are more complex cases in which swapping colors won’t help to get from one coloring to the other.

In the following picture taken from http://en.wikipedia.org/wiki/Graph_coloring, the graphs named (A) and (B) are the only ones that cannot be converted into one another by swapping colors.

In particular I’m interested in regular maps, excluding all maps that can be colored with 2 or 3 colors. For what I need to analyze, maps have to be regarded as differently colored, if the same coloring cannot be obtained by subsequent exchanges of colors.

In other words, for example, once a map has been properly colored, I don’t want to count all other configurations that derive from subsequent exchanges of colors.

Since the arbitrary nature of choosing colors, these derived configurations are equivalent (for what I’m analyzing) to the first one, since they could have been obtained just choosing different colors in the first place. Instead, there are colorings that differ in such a way that exchanging colors won’t help to transform one configuration into the other.

My question is: how many “different” colorings (in the meaning I explained) exist for a given map?

I’ve only found an article on http://en.wikipedia.org/wiki/Graph_coloring that count all possible colorings including swaps.

Is there a paper that can help me on this?

T1 was already known

Posted on April 2, 2011 by stefanutti

The theorem I proved in T1 was already known. It was found by Kempe back in 1879 in terms of graph theory (see http://en.wikipedia.org/wiki/Four_color_theorem: “Kempe also showed correctly that G can have no vertex of degree 4″). Only 132 years later … not bad.

People from http://cstheory.stackexchange.com helped me on this (to find that it was already known). See here: http://cstheory.stackexchange.com/questions/5822.

I still think my proof it is of some value, since it is not expressed in terms of graph theory (of the dual graph derived from the map).

Four color theorem: music is on

Posted on March 24, 2011 by stefanutti

When coloring maps using the Java application each color can play a different instruments with different parameters.

Download the application and play it yourself: https://github.com/stefanutti/maps-coloring-java.

Or turn on the speakers and watch this video:

Four color theorem: slow motion maps

Posted on March 21, 2011 by stefanutti

Here is a video that shows the nature of rectangular and circular maps.

All maps concerning the four color theorem (“regular maps” | “planar graphs without loops”) can be topologically transformed into rectangular and circular maps.

Four color theorem: which one is the correct graph?

Posted on March 18, 2011 by stefanutti

Wikipedia: “In graph-theoretic terminology, the four-color theorem states that the vertices of every planar graph can be colored with at most four colors so that no two adjacent vertices receive the same color, or for short, every planar graph is four-colorable.”

But exactly which kind of planar graphs have to be considered?:

Without loops
What about multiple edges? Why are these often excluded?

Four Color Theorem

Four Color Theorem, Guthrie, Kempe, Tait, Heawood and other people and stuff

Tag Archives: four colors suffice