This post follows directly the previous one. I’m down to a single case to prove (pag. 3).
I think I should move to Java coding, implementing the entire algorithm: map reduction (removing edges), color reduced map, restore of edges one at a time, adjust the coloring to the case to prove (e2 = red), apply Kc5 color switching, …, apply the half Kempe-cycle color switching.
Notes (pag. 1 and 2):
Second page:
Finally I bought two books about the four color theorem: “Four Colors Suffice: How the Map Problem Was Solved” by Robin Wilson e Ian Stewart; and the “The Four-Color Theorem: History, Topological Foundations, and Idea of Proof” by Rudolf Fritsch and Gerda Fritsch.
I am currently reading the first one, and I want to revisit the fundamentals by using the method Kempe employed when he believed he had solved the problem.
With these differences: I will approach it removing one edge at a time from F2, F3, F4, or F5 faces (unavoidable set) to reduce the map to two faces (including the ocean). Afterward, I will restore the edges in reverse order, consistently working with 3-regular planar graphs. Instead of applying Kempe’s chain color switching solely to the faces, I will consider Tait coloring of the edges and apply Kempe’s chain color switching to the edges.
Follow the arrow to visualize the steps:
It is known that for regular maps, “3-edge coloring” is equivalent to finding a proper “four coloring” of the faces of a map.
This post is about coloring impasses, fallacious Kempe chain color swapping (not solving the impasse) and an hypothesis I’d like to verify.
FIRST: What is an impasse
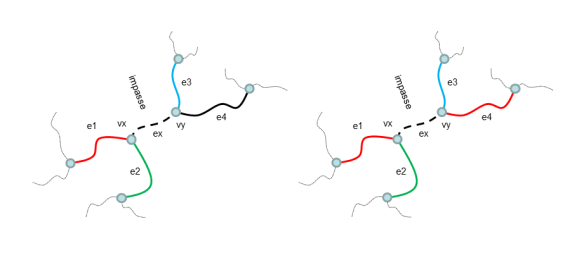
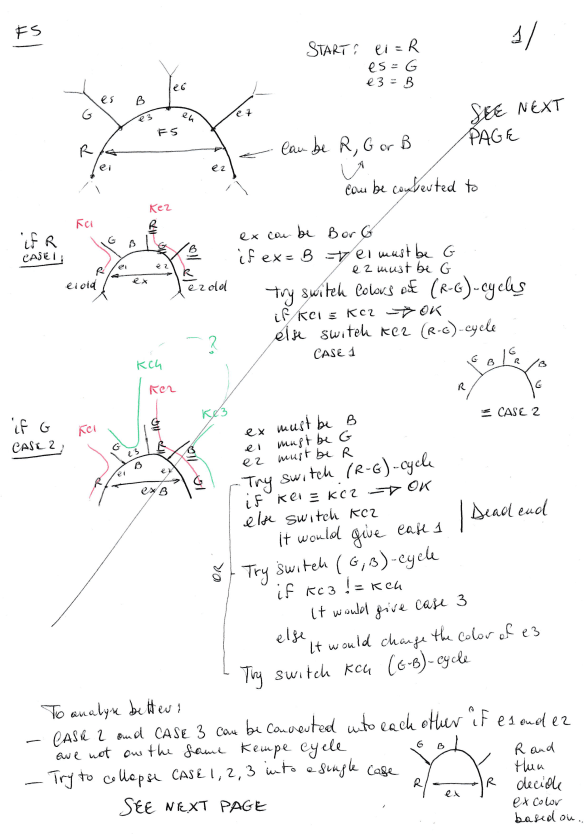
Lets say you are coloring (Red, Green, Blue) the edges of a map and have properly colored a portion of it, as in the example. At a certain point you get to a vertex that has two edges already colored, for example with Red and Green (e1, e2). In this case you’d be forced to select the color Blue for the uncolored edge (ex). But it is possible that the color Blue is already used by one of the other two edges starting from vy (e3). This situation is called impasse. In the example e4 may be already colored or not, the impasse remains.
SECOND: Apply Kempe chain color swapping and problems using it
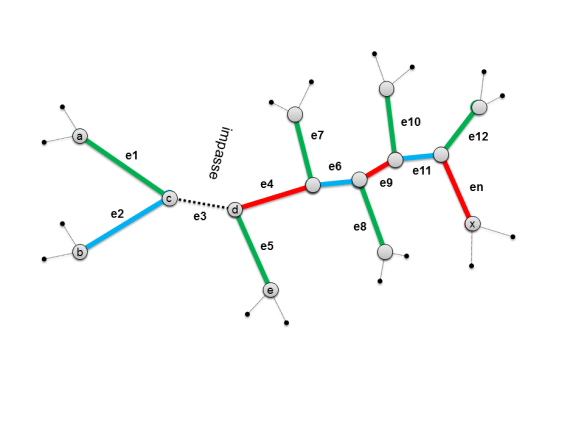
One technique that can be used to solve an impasse is to apply a Kempe chain color swapping. But the problem is that this Kempe swap does not always work. This happens when the Kempe swap does not only change the color of the edge that caused the impasse (e4), but also the color of one of the other three edges involved in the impasse (e1, e2, e5 in the example).
To better understand Kempe chain color swapping, lets analyze, step by step, the labeled part the graph showed above:
THIRD: Hypothesis to solve the second impasse when Kempe swap fails
Using the Java application I wrote, I started experimenting Kempe chain color swapping and found many situation where the swapping would not solve the impasse, but I also found a method, which of course needs to be proved, to solve the second impasse when Kempe chain color swapping fails (fallacious Kempe chain color swapping). If true (consider that what is written in this blog are just personal notes about an attempt) this would prove the four color theorem a very short and elegant way.
<insert video>
Hypothesis:
The hypothesis I’d like to verify is that from maps in which F2, F3, F4 faces have been previously removed (which is safe for the proof of the theorem), the fallacious Kempe chain can always be “broken” (or in different words: its path changed) along the way (using another Kempe chain coloring swap) to avoid the second impasse. After this “cut”, the original swap can be performed to solve the original impasse.
I tried this method on many maps with and without F2, F3, F4 faces, and so far it seems to work … always.
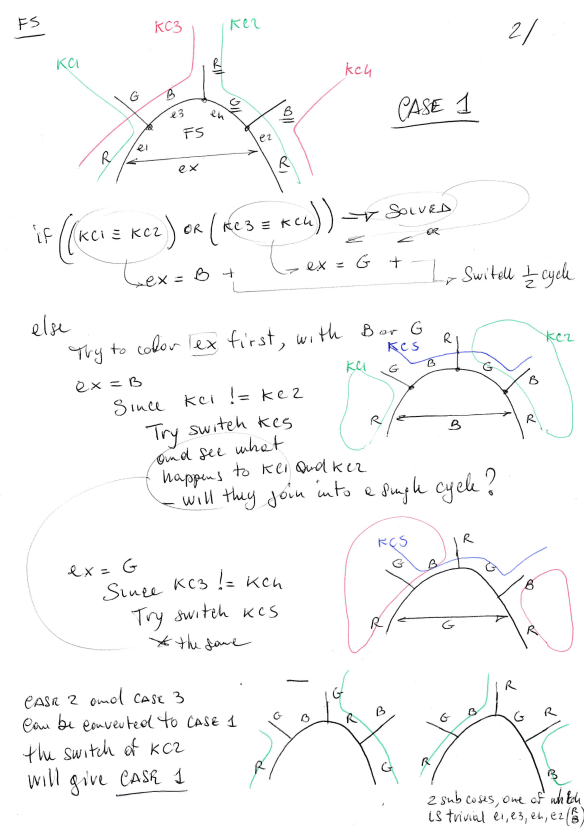
Here is an example:
In this example:
To be finished:
😦
Too many more things to do and little time:
Bye
And here is the video that shows how to get a Tait colored map (graph) from a rectangular map.
From Wikipedia: “The four color theorem, on vertex coloring of planar graphs, is equivalent to the statement that every bridgeless 3-regular planar graph is of class one (Tait 1880). This statement is now known to be true, due to the proof of the four color theorem by Appel & Haken (1976).”
Here is a simple implementation of this equivalence, that converts a map from “4-face-colored” to “3-edge-colored”.
Here is the link to try the new functionality: https://github.com/stefanutti/maps-coloring-java/releases/download/4ct/ct-ui-swixml-2.3-jar-with-dependencies.jar
Four Color Theorem 