Tag Archives: pencil and paper

3-regular planar graph decomposition in cycles and 4CT

Posted on by
Reply

If you can prove that it is possible to decompose a 3-regular graph into cycles, all with even length, you have also proved the four color theorem.

I think this fact is already known, but I never paid too much attention to it before.

Naturally, also the opposite is true: since the 4CT is true, it means that it is possible to color it, and also get the Tait coloring. And for any two colors you choose (for example Red and Green), the related Kempe cycles form a partition of the graph and each cycle has an even number of edges.

Once the decomposition is found, since the cycles have an even number of edges, it is possible to color the edges of a cycle with two alternate colors (for example Red and Green), forming this way Kempe cycles. When all cycles are colored (with R and G), it is possible to use a third color (for example Blue) to color the remaining edges.

The resulting graph will have a Tait coloring for all edges, which is equivalent to coloring all faces with four different colors.

But, how difficult is it to find all cycles?

This one has 6 Red-Green cycles (all of even length), that form a division on the 3-regular planar graph into cycles.

Non-Hamiltonian 3-regular planar graphs, Tait coloring and Kempe cycles … what else ;-)

Posted on by
Reply

Considering the smallest known non-Hamiltonian 3-regular planar graphs, discovered by Barnette-Bosák-Lederberg, I computed the Tait coloring and then deformed it to put in evidence the R-G cycles that in this case are four.

Links to the historical importance of this graph:

https://mathworld.wolfram.com/Barnette-Bosak-LederbergGraph.html

https://en.wikipedia.org/wiki/Barnette–Bosák–Lederberg graph

And here is the Tait coloring of this graph:

Deformed here to better show the R-G cycles:

Tait coloring and the four color theorem: personal Q&A

Posted on by
Reply

Some questions about the previous post:

Q1) Can cycles be concentric?

Yes, see this example.

Q2) Verify if at least one of the cycles (R-G, R-B, or G-B) form an Hamiltonian circuit

False.

From the Tait’s conjecture we now know (now = 1946 by William Thomas Tutte) that 3-regular graphs exist also without an Hamiltonian circuit. It means that, no matter what, it is not possible to find a cycle that touches all vertices, and therefore no single Kempe cycles of any two color selection, can exist.

From Wikipedia, the free encyclopedia

This article is about graph theory. For the conjectures in knot theory, see Tait conjectures.

In mathematics, Tait’s conjecture states that “Every 3-connected planar cubic graph has a Hamiltonian cycle (along the edges) through all its vertices“. It was proposed by P. G. Tait (1884) and disproved by W. T. Tutte (1946), who constructed a counterexample with 25 faces, 69 edges and 46 vertices. Several smaller counterexamples, with 21 faces, 57 edges and 38 vertices, were later proved minimal by Holton & McKay (1988). The condition that the graph be 3-regular is necessary due to polyhedra such as the rhombic dodecahedron, which forms a bipartite graph with six degree-four vertices on one side and eight degree-three vertices on the other side; because any Hamiltonian cycle would have to alternate between the two sides of the bipartition, but they have unequal numbers of vertices, the rhombic dodecahedron is not Hamiltonian. The conjecture was significant, because if true, it would have implied the four color theorem: as Tait described, the four-color problem is equivalent to the problem of finding 3-edge-colorings of bridgeless cubic planar graphs. In a Hamiltonian cubic planar graph, such an edge coloring is easy to find: use two colors alternately on the cycle, and a third color for all remaining edges. Alternatively, a 4-coloring of the faces of a Hamiltonian cubic planar graph may be constructed directly, using two colors for the faces inside the cycle and two more colors for the faces outside.

Smallest known non-Hamiltonian 3-regular planar graph: https://mathworld.wolfram.com/Barnette-Bosak-LederbergGraph.html.

Next post will be on the four coloring of the barnette-bosák-lederberg graph, which is the smallest known non-Hamiltonian graph, and the analysis of its Kempe cycles.

Q3) What about if I start with finding cycles, of even length (# of edges), that cross all vertices?

Some initial considerations: If cycles have to fit with Kempe cycles (closed paths of two alternating colors), they have to be of even length, and that would also mean that the total number of vertices crossed by all the cycles of the same two colors should be even too. Is it like this, or am I missing something? What about graphs with an odd number of vertices? Am I missing something?

Answer to the initial consideration: https://math.stackexchange.com/questions/181833/proving-that-the-number-of-vertices-of-odd-degree-in-any-graph-g-is-even + https://math.stackexchange.com/questions/181833/proving-that-the-number-of-vertices-of-odd-degree-in-any-graph-g-is-even

Finding cycles seems to be as difficult as finding a solution for of 4 coloring problem 😦

New paths for the 4ct?

Posted on by
Reply

The other day, before going to sleep, I realized that I needed to revisit the problem, starting with a piece of evidence I had noticed long ago. When a map is colored, the corresponding Tait coloring of the borders creates color chains (R-G, R-B, or G-B) that always form loops. Moreover, there may be more than one loop for each pair of colors. For example, the map shown here has:

1 R-G loop

  • 190, 557, 776, 525, 527, 126, 92, 76, 75, 84, 613, 770, 765, 170, 55, 61, 32, 15, 16, 10, 745, 712, 590, 756, 775, 6, 30, 57, 190

2 R-B loops

  • 190, 557, 765, …, 756, 190
  • 745, 712, 527, 126, 16, 10, 6, 775, 745

2 G-B loops

  • 190, 57, 55, 170, …, 756, 190
  • 776, 557, 765, 770, 525, 527, 712, 590, 776
Four color theorem

I wonder if analyzing how these loops form during the rebuilding phase of a map, after the reduction phase (see other posts), can lead me out of the mud.

Notes:

  • Once the map is completely four-colored (or 3-edge colored = Tait coloring), each chain (two-color chain) is actually a loop
    • This becomes clear when you consider the colors available at each vertex as you follow a chain. For example, if you’re examining the R-G chain and start from a vertex, following the Red color to the next vertex, that vertex will have the Green color available to continue the chain. As you keep alternating between R and G, each new vertex will offer the other color in the chain until you eventually return to the starting vertex, thereby closing the loop
  • If only one chain for a specific color selection (R-G, R-B, or G-B) exists, that chain touches all vertices of the map
    • If it weren’t so, one of the vertices not on the chain still would have the edges colored with three different colors, two of which (the same two colors of the chosen chain) would form another chain
  • The length of all loops is always an even number
    • This come straightforward from the definition of chain, multiple sequences of R and G = 2n

Deforming the original map, I managed to put in evidence the R-G loop, and then the other loops (R-B and G-B) respect to the first R-G deformation.

And here with the loops filled

Additional note:

This was the map when I discovered that infinite random switches throughout the entire graph do not solve the impasse. It was bad 😦 The graph here is identical to the one in the previous post.

https://four-color-theorem.org/2016/10/31/four-color-theorem-infinite-switches-are-not-enough/

Four color theorem: other representations of maps

Posted on by
Reply

Here are some new representation of graphs:

Thanks to:

Four color theorem: representations of maps

Posted on by
5

For the scope of the four color problem and without lack of generality, maps can be represented in different ways. This is generally done to have a different perspective on the problem.

For example, the graph-theoretic representation of maps has become so common and important that generally the four color problem is stated and analyzed directly in terms of graph theory: http://en.wikipedia.org/wiki/Four_color_theorem.

I am trying to collect other representations that may in some way help to get a different point of view on the problem. If you know one of these representations that is not listed and wish to share, report it here. If you also have a web reference that explains or shows the representation, it would be great.

The representations have to be general and applicable to all maps with the simplification that only regular maps (no exclaves or enclaves, 3 edges meeting at each vertex, etc.) can be considered.

These are some classic representations:

  • Natural: As a 3-regular planar graph (boundaries = edges)
  • Canonical: As the dual graph of the “natural” representation (region = vertex, neighbors = edges)
  • As a straight line drawing graph (Fáry’s theorem)
  • As a graph with vertices arranged on a grid
  • As a rectilinear cartogram

Plus, I found these:

  • As a circular map
  • As a rectangular map
  • As clefs (derived from rectangular maps)
  • As pipes map (derived from the clefs representation)
  • …

New representations (answers from mathoverflow):

Here is an example of some of these representations for the original map shown:

See next post for other representations.

Counting maps

Posted on by
Reply

I’ve posted this question on mathoverflow.

Is there a formula to count how many different topological regular maps can be created with n faces (on a sphere)?

  • For “regular” I intend maps in which the boundaries form a 3-regular planar graph
  • For “different” I intend maps that cannot be topologically transformed one into another (faces have to be considered unnamed)

I’ve been looking for a formula, but it is too difficult for me. Maybe it has a simple solution but I don’t see it.

This was my best guess, but I already know that it is not correct because full of symmetries, as it can be verified manually.

General formula:

2\sum _{s_{(f-3)}=2f-5}^{2f-5+2} \text{...}\sum _{s_3=7}^{s_4} \sum _{s_2=5}^{s_3} \sum _{s_1=3}^{s_2} s_1\left(s_1-1\right)\left(s_2-3\right)\left(s_3-5\right)\text{...}\left(s_{(f-3)}-((2f-5)-2)\right)

4 faces = 2\sum _{s_1=3}^5 s_1\left(s_1-1\right)
5 faces = 2\sum _{s_2=5}^7 \sum _{s_1=3}^{s_2} s_1\left(s_1-1\right)\left(s_2-3\right)

Here are the first results that can be found manually (excluding simmetrical maps):

  • 2 faces = 0 possible regular map (an island and the ocean) (not to be counted, because not regular)
  • 3 faces = 1 possible regular map (an island with two regions and the ocean) (two islands and the ocean wouldn’t be regular)
  • 4 faces = 3 possible regular maps (can be verified adding a face from the previous map)
  • 5 faces = 16 possible regular maps (with homeomorphics eliminated)
  • …

These are all maps up to 5 faces:

Are these different colorings?

Posted on by
Reply

UPDATE (18/Apr/2011)

The nunber of proper colorings (not considering permutations of colors) can be count using the “Chromatic polynomial” and dividing the result by 4! (factorial that counts the permutations). But, the chromatic polynomial is only known for few types of graphs (Triangle K3, Complete graph Kn, Petersen graph, …). I haven’t found papers on this problem. Highly propably, since the difficulty to find the Chromatic polynomial of complex graphs, there cannot be a direct formula to calculate how many different colorings exist.

I’ve posted this question here on mathoverflow.

END UPDATE

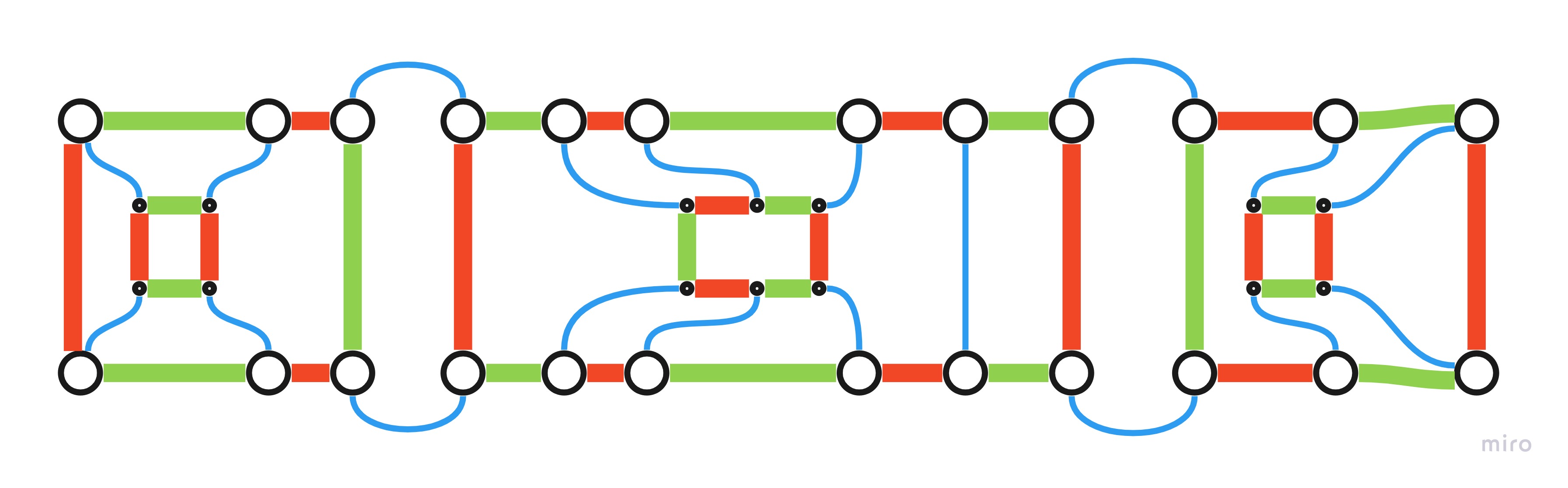
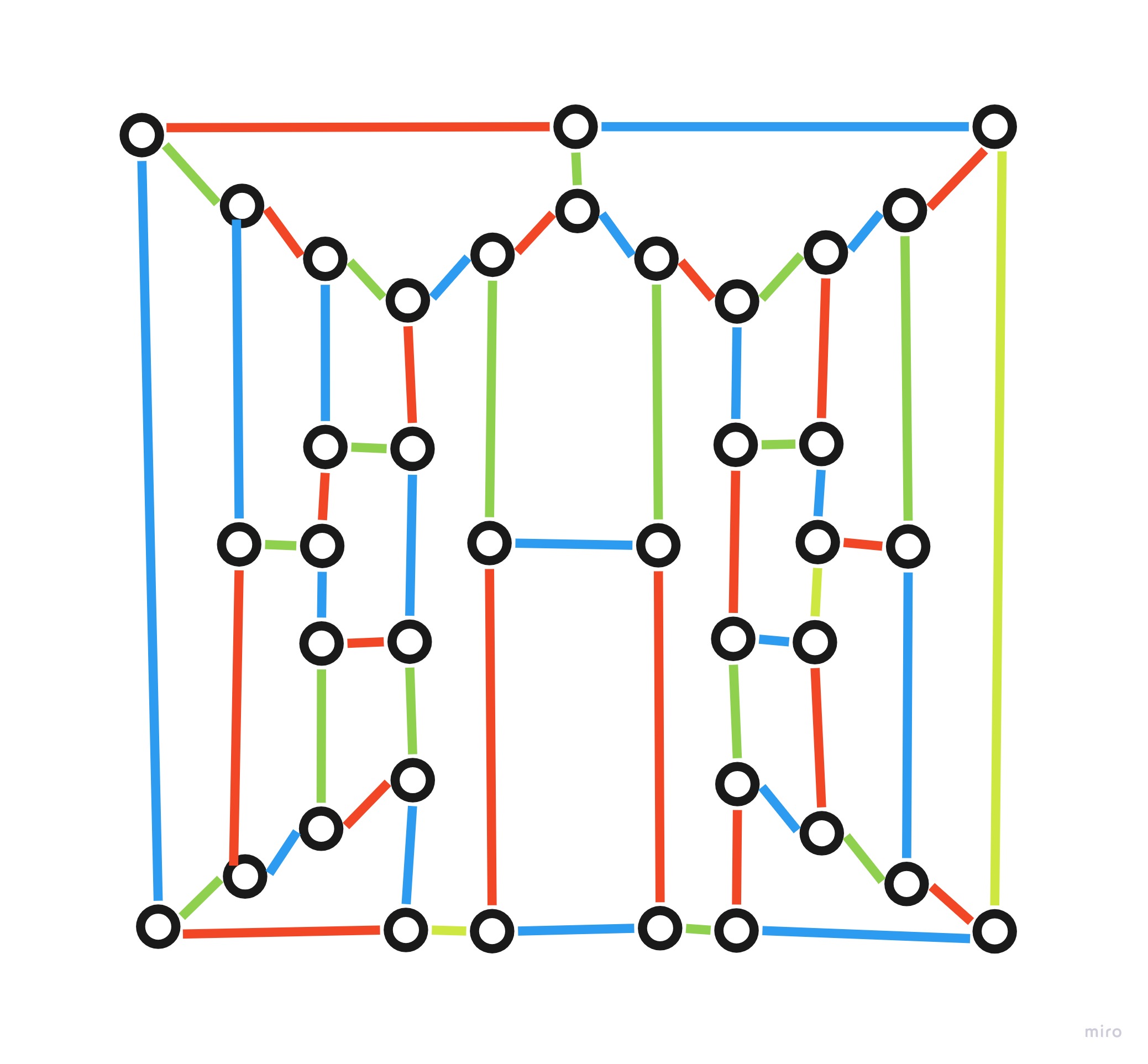
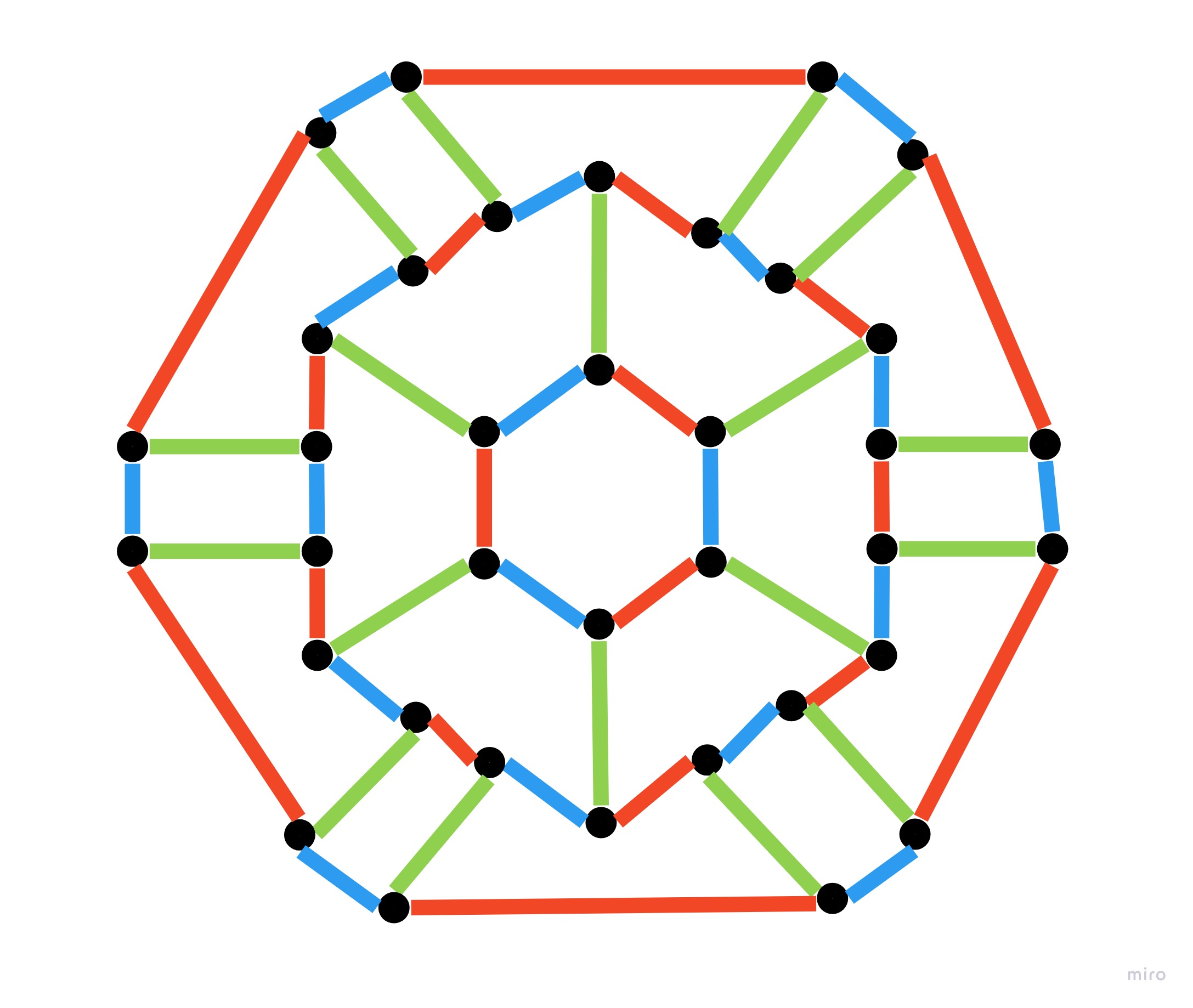
Take a look at these three graphs:

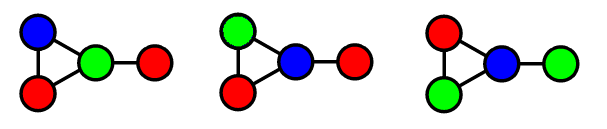
Are these really different colorings?

Before to dismiss this, do the following on the first graph:

  • Change Blue to Yellow (Blue was just an arbitrary color among infinite others)
  • Change Green to Blue
  • Change Yellow to Green

Now you have the second graph. Continue with this:

  • Change Green to Yellow
  • Change Red to Green
  • Change Yellow to Red

Now you have the third graph. Since the arbitrary nature of the choice of colors, the first graph could have been colored as the third one since the beginning.

The same result, can be obtained by changing all three colors of the first graph to three other colors. If applying the same method to the third graph, you can get the same configuration for the two graphs, it means that they can be considered, for some areas of investigation, as the same configuration.

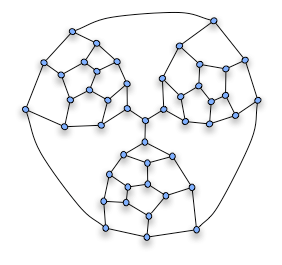
There are more complex cases in which swapping colors won’t help to get from one coloring to the other.

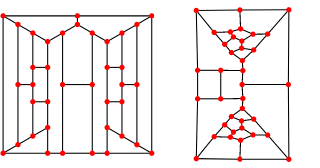
In the following picture taken from http://en.wikipedia.org/wiki/Graph_coloring, the graphs named (A) and (B) are the only ones that cannot be converted into one another by swapping colors.

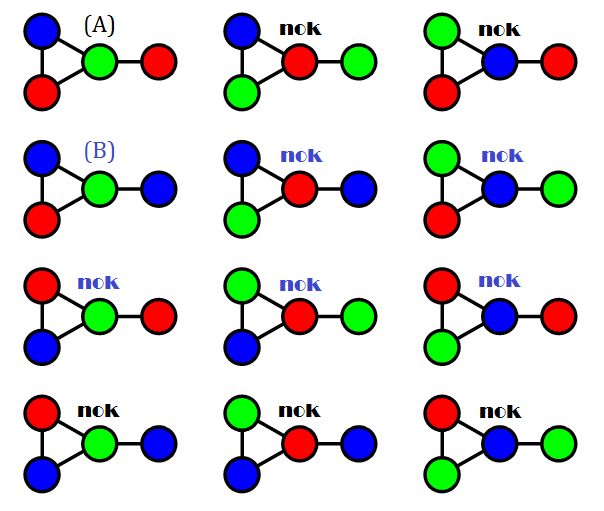
In particular I’m interested in regular maps, excluding all maps that can be colored with 2 or 3 colors. For what I need to analyze, maps have to be regarded as differently colored, if the same coloring cannot be obtained by subsequent exchanges of colors.

In other words, for example, once a map has been properly colored, I don’t want to count all other configurations that derive from subsequent exchanges of colors.

Since the arbitrary nature of choosing colors, these derived configurations are equivalent (for what I’m analyzing) to the first one, since they could have been obtained just choosing different colors in the first place. Instead, there are colorings that differ in such a way that exchanging colors won’t help to transform one configuration into the other.

My question is: how many “different” colorings (in the meaning I explained) exist for a given map?

I’ve only found an article on http://en.wikipedia.org/wiki/Graph_coloring that count all possible colorings including swaps.

Is there a paper that can help me on this?

Four color theorem: music is on

Posted on by
Reply

When coloring maps using the Java application each color can play a different instruments with different parameters.

Download the application and play it yourself: https://github.com/stefanutti/maps-coloring-java.

Or turn on the speakers and watch this video: