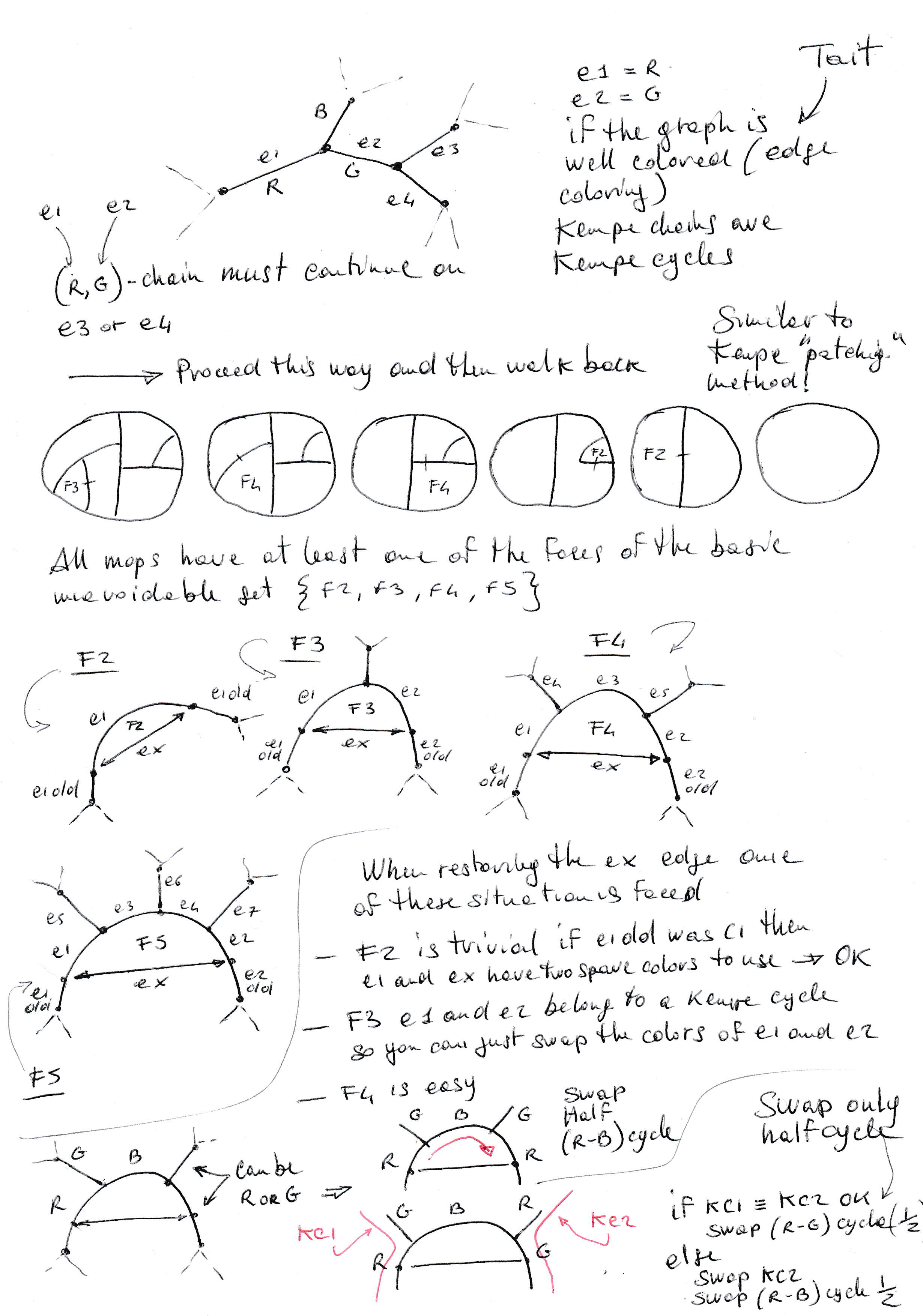
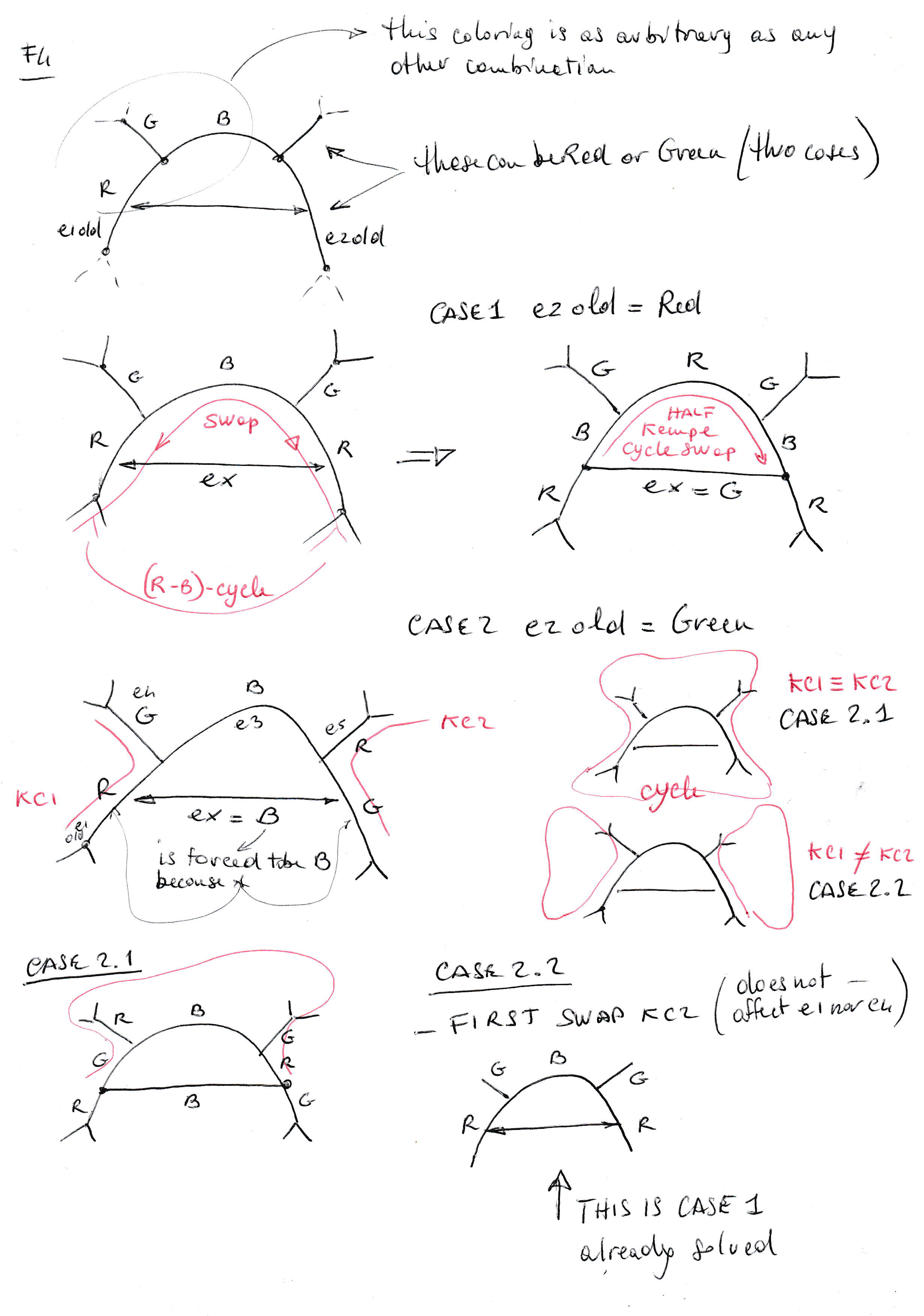
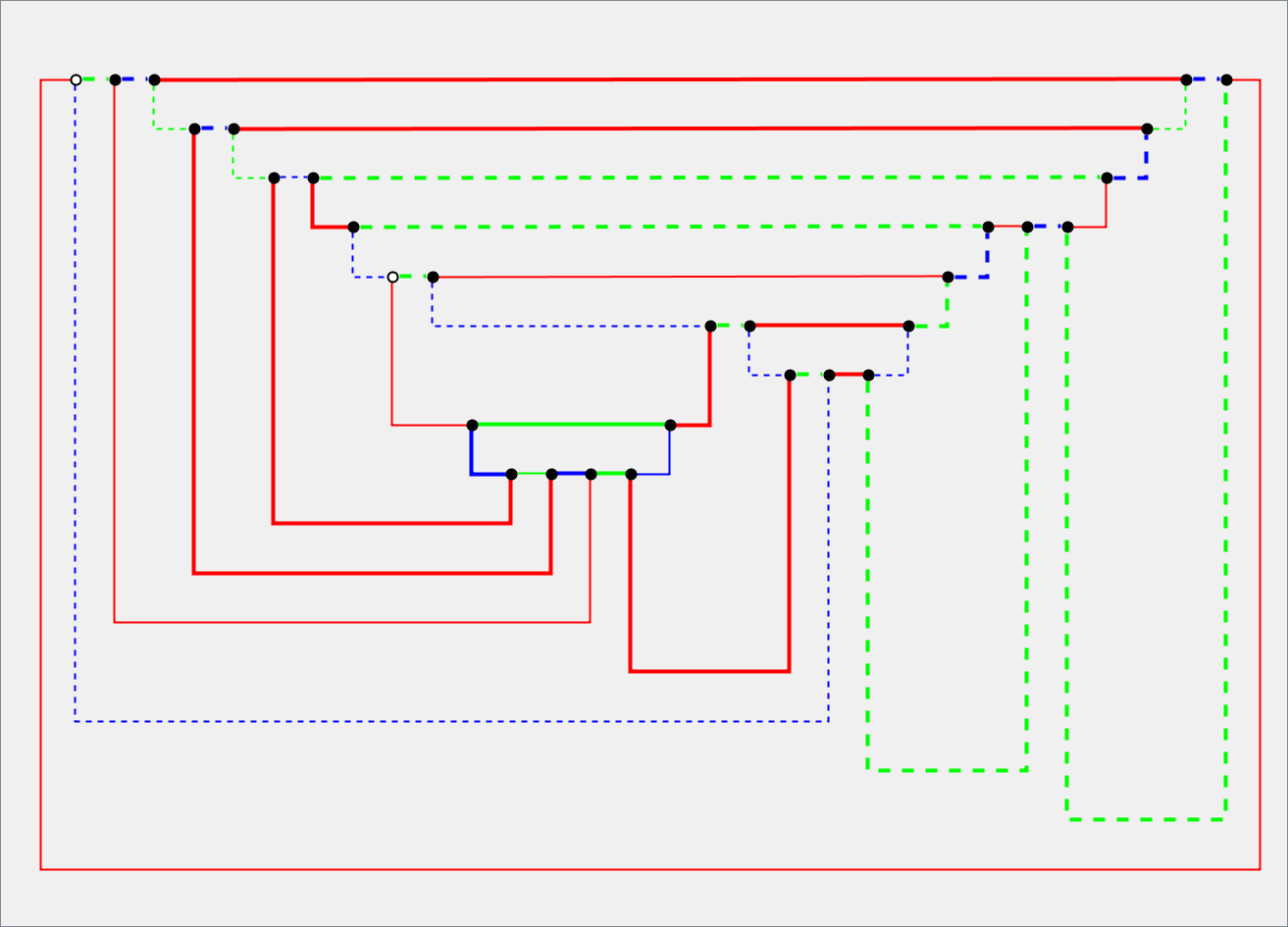
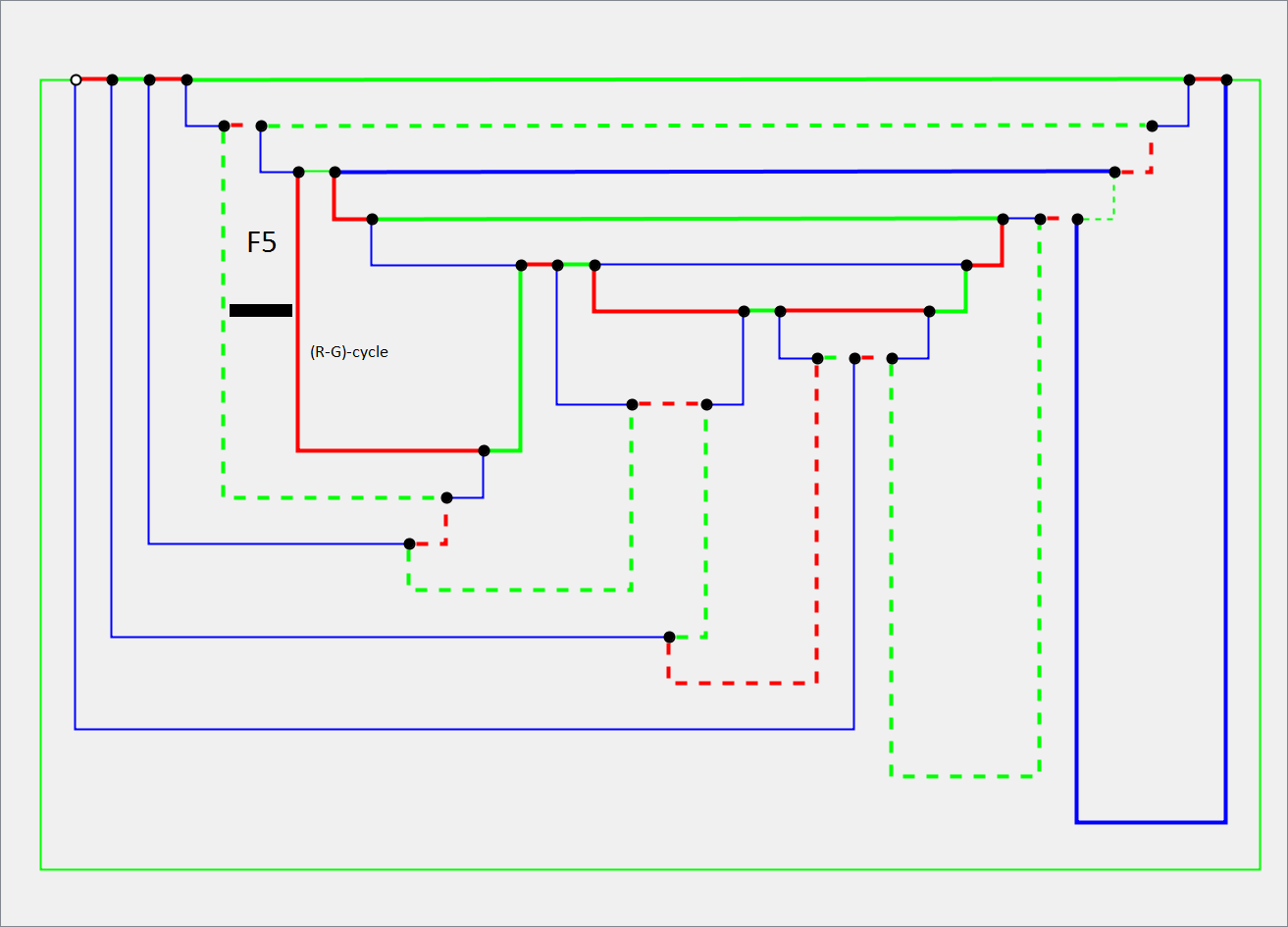
During the process of removing faces from a planar map (cubic planar graph) this video shows how the Euler’s equation redistribute its weights:
+4F2 +3F3 +2F4 +1F5 +0F6 -1F7 -2F8 -3F9 …. = 12
The map that has been used to produce this video is represented by a planar cubic graph made of almost 10000 faces (20000 vertices and 27972 edges).
The selection for the edges to remove that I used was: take an edge from an F2. Then, if no F2 exist, use an F3. And then, if no F3 exist, use an F4 and finally an F5.
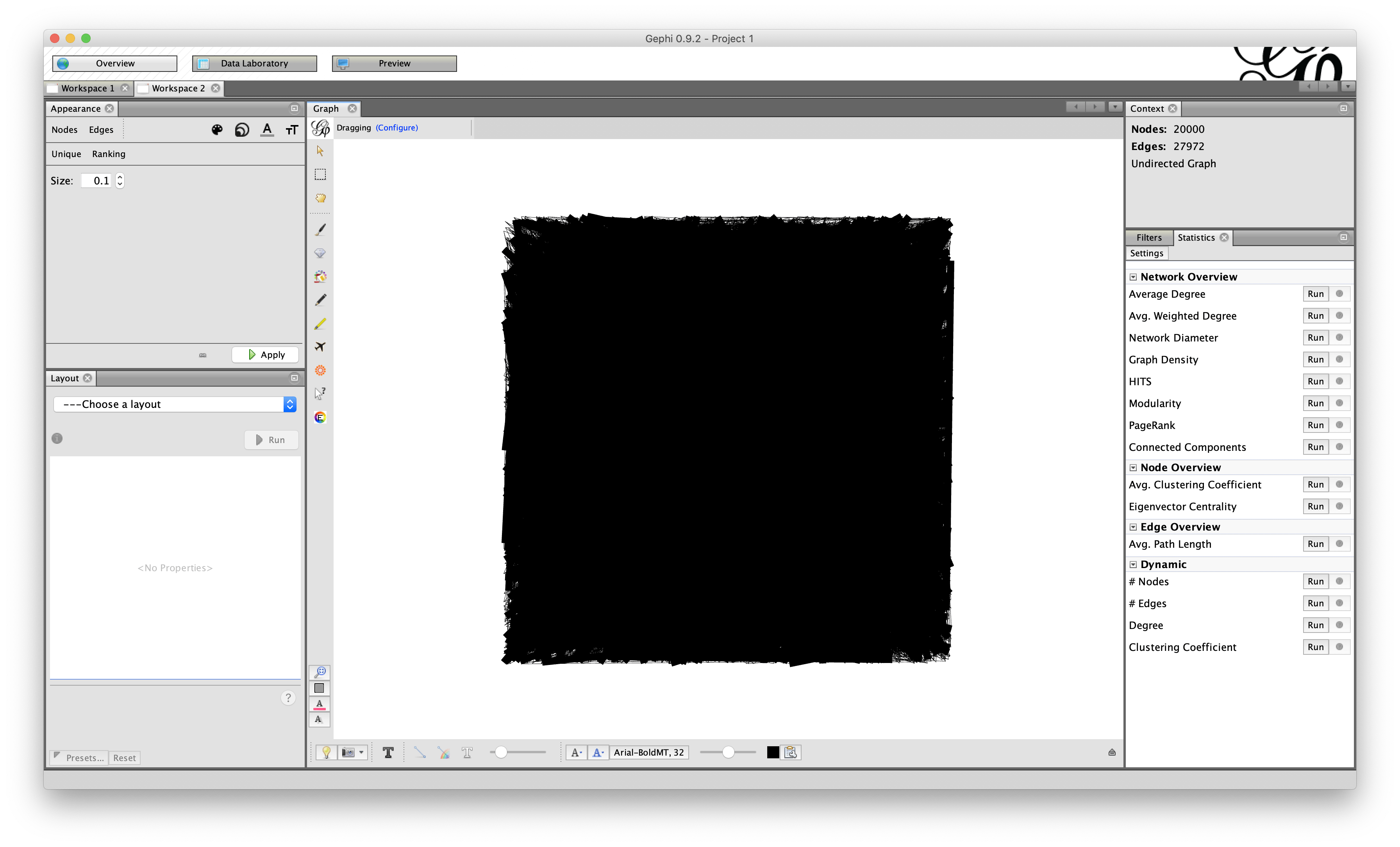
Here is the .dot file and the planar representation of the map.
Return it to me Tait coloured if you can 🙂
mailto:mario.stefanutti@gmail.com?subject=4CT Tait coloring
Meaning with all edges using only three colours (without conflicts at the vertices), which is equivalent to color the faces with four colours.
Bye
PS:
2020-04-26 22:37:21,310 - root - INFO - ------------------
2020-04-26 22:37:21,310 - root - INFO - BEGIN: Print stats
2020-04-26 22:37:21,310 - root - INFO - ------------------
2020-04-26 22:37:21,311 - root - INFO - Stat: CASE-F2-01 = 4114
2020-04-26 22:37:21,311 - root - INFO - Stat: CASE-F3-01 = 4478
2020-04-26 22:37:21,311 - root - INFO - Stat: CASE-F4-01 = 732
2020-04-26 22:37:21,311 - root - INFO - Stat: CASE-F4-02 = 442
2020-04-26 22:37:21,311 - root - INFO - Stat: CASE-F4-03 = 231
2020-04-26 22:37:21,311 - root - INFO - Stat: CASE-F5-C1!=C2-SameKempeLoop-C1-C2 = 1
2020-04-26 22:37:21,311 - root - INFO - Stat: CASE-F5-C1==C2-SameKempeLoop-C1-C3 = 1
2020-04-26 22:37:21,312 - root - INFO - Stat: CASE-F5-C1==C2-SameKempeLoop-C1-C4 = 0
2020-04-26 22:37:21,312 - root - INFO - Stat: MAX_RANDOM_KEMPE_SWITCHES = 0
2020-04-26 22:37:21,312 - root - INFO - Stat: TOTAL_RANDOM_KEMPE_SWITCHES = 0
2020-04-26 22:37:21,312 - root - INFO - Stat: time_ELABORATION = 1015
2020-04-26 22:37:21,312 - root - INFO - Stat: time_ELABORATION_BEGIN = Sun Apr 26 22:19:55 2020
2020-04-26 22:37:21,313 - root - INFO - Stat: time_ELABORATION_END = Sun Apr 26 22:36:50 2020
2020-04-26 22:37:21,313 - root - INFO - Stat: time_GRAPH_CREATION_BEGIN = Sun Apr 26 22:19:22 2020
2020-04-26 22:37:21,313 - root - INFO - Stat: time_GRAPH_CREATION_END = Sun Apr 26 22:19:55 2020
2020-04-26 22:37:21,313 - root - INFO - ----------------
2020-04-26 22:37:21,314 - root - INFO - END: Print stats
2020-04-26 22:37:21,314 - root - INFO - ----------------