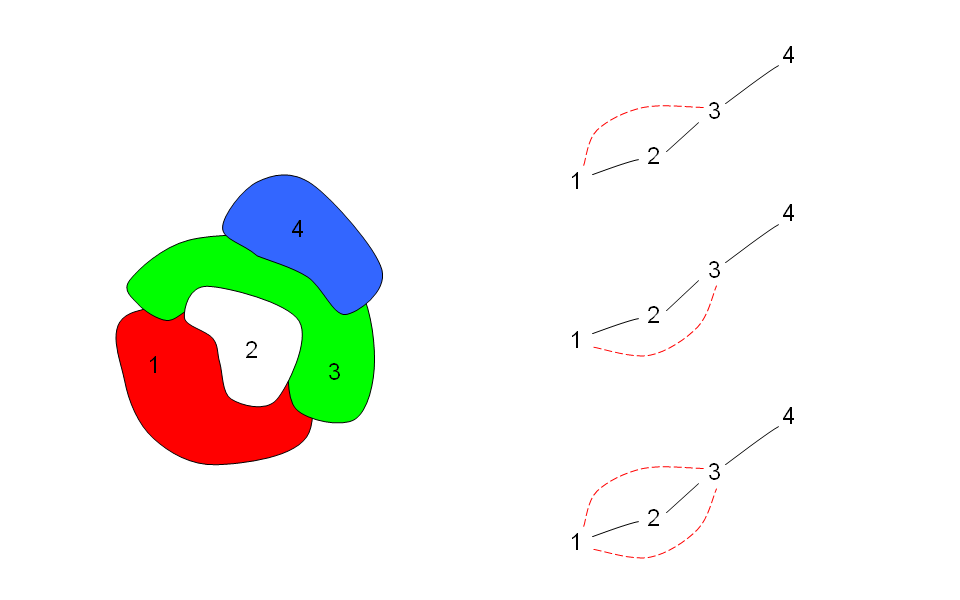
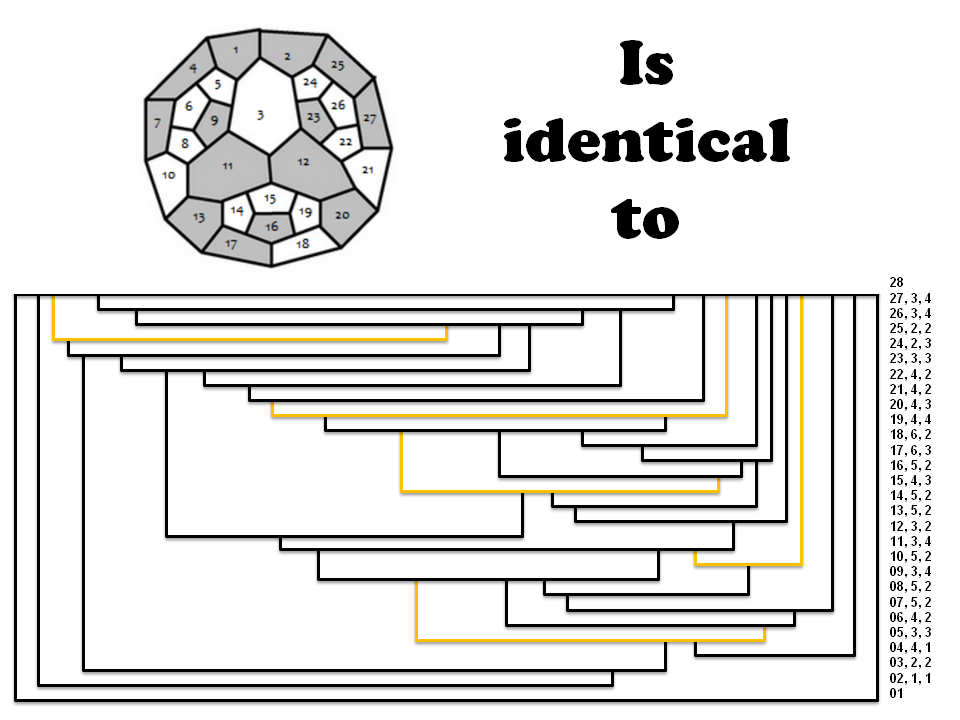
The theorem I proved in T1 was already known. It was found by Kempe back in 1879 in terms of graph theory (see http://en.wikipedia.org/wiki/Four_color_theorem: “Kempe also showed correctly that G can have no vertex of degree 4″). Only 132 years later … not bad.
People from http://cstheory.stackexchange.com helped me on this (to find that it was already known). See here: http://cstheory.stackexchange.com/questions/5822.
I still think my proof it is of some value, since it is not expressed in terms of graph theory (of the dual graph derived from the map).