I just realized the the 7 bridges of Königsberg are now only 5.
How sad.
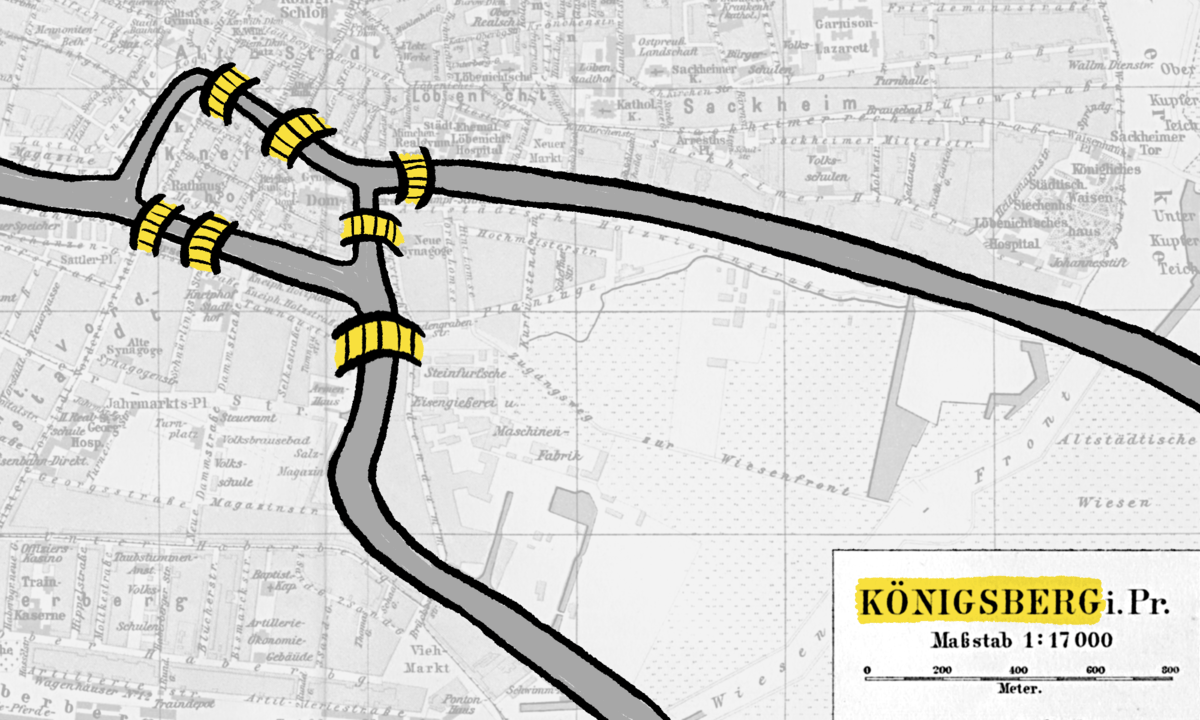
Zoom it yourself 😦 https://earth.app.goo.gl/9UazXP
Some historical information about the problem:
Really hope someone is the future will rebuild those 2 missing bridges.
The four color theorem appeared in 1852, talking about the problem of coloring real maps. Let’s examine some basic aspects of these maps in relation to the four color theorem.
A world with just water and one land with no divisions, topologically equivalent to a disk, needs only two colors to paint the land and the ocean. This is the beginning, as the Pangea on Earth long ago.
If two parties want to share this land and both want to have access to the ocean and have contiguous regions, there is only one possible configuration, and the resulting map can be represented by a planar graph with 2 vertexes and 3 edges (multiedge graph). The other solutions that have been excluded by the two restrictions: “have access to the ocean” and “contiguous regions” are not so interesting for the scope of the theorem (see previous post).
If a third party comes into play, the initial region (surrounded by the ocean) has to be split among three parties, with the same two restrictions as stated before: “have access to the ocean” and “be contiguous regions”. If we consider all possible combinations, we can also see that among them there are some that can be eliminated introducing a third rule: “all faces have to touch each other”. This third rule can be added because all the configurations in which the three faces don’t touch each other contain F2 faces and therefore (is it to be proved?) can be eliminated. It will then rest only one configuration that meet all criteria, that is the one printed at the bottom right of the previous post image.
There are some methods around to create planar graphs. One of these is based on the Delaunay triangulation algorithm from which you can derive its dual, a 3 regular planar graph. Tools and libraries that I found around (sage, networkx and others), permits you to save the graph using one of common format to represent the graph itself, specifically: .dot, .graphml, .GEXF, .gpickle and others). One problem that I found is that if I save the graph I loose the planar representation of it.
Since for what I am trying to do, namely demonstrate with pencil and paper that the four color theorem has a simpler demonstration, I need to work directly with the planar representation of the graph.
I decided to implement my own method (based on edge addition to planar graphs. See “John M. Boyer and Wendy J. Myrvold, On the Cutting Edge: Simplified O(n) Planarity by Edge Addition. Journal of Graph Algorithms and Applications, Vol. 8, No. 3, pp. 241-273, 2004.”) to generate an save the graph directly using its planar representation. Get the code here at: https://github.com/stefanutti/maps-coloring-python. The program generates random planar graphs without using graphs library and most importantly without using complex algorithms, as planar embedding or planarity testing.
Planar embedding: “A combinatorial embedding of a graph is a clockwise ordering of the neighbors of each vertex. From this information one can define the faces of the embedding”.
sage: T = graphs.TetrahedralGraph()
sage: T.faces({0: [1, 3, 2], 1: [0, 2, 3], 2: [0, 3, 1], 3: [0, 1, 2]})
[[(0, 1), (1, 2), (2, 0)],
[(3, 2), (2, 1), (1, 3)],
[(3, 0), (0, 2), (2, 3)],
[(3, 1), (1, 0), (0, 3)]]
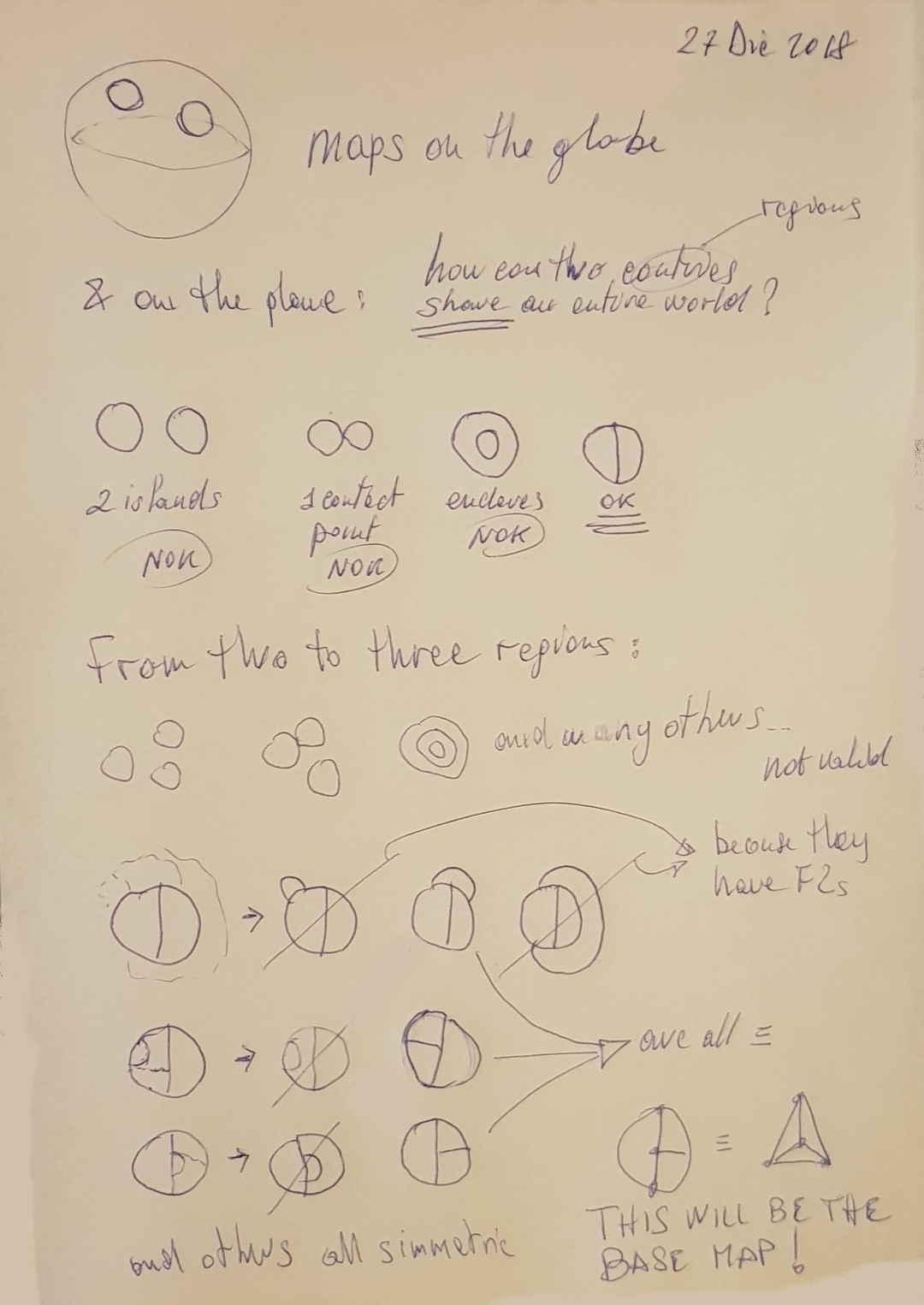
Edge addition can start from a basic graph of four faces (bottom right). In the third last line of this picture I added edges from a graph with 3 faces and 2 vertices (considering the ocean). But as you can deduct from the other pictures I can safely start from a graph with 4 faces and 4 vertices (bottom right).
These are the OLD and NEW (last column) execution times on my new laptop:
I moved all code under github here: https://github.com/stefanutti
For the decomposition of a graph representing a map, I’m trying to use different algorithms to select the edge to remove.
The question is:
Some basic rules are:
Here are all possibilities. Last 2 groups (removing edges from F5 and F6) don’t have to be taken into account. I just wanted to see how it continued after the cases with faces made of 2, 3, 4 and 5 edges:
This is what I want to try:
The rule: avoid F5 or at least do not create them.
Other to avoid:
NOTE:
The algorithm I use to color graphs works pretty well … BUT:
So, what now?
I want to try other strategies while removing edges from the original graph, to avoid the above condition. I want to eliminate the need of random swithes.
The sequence I used so far is:
I want to try:
A planar cubic graphs to visualize what I wrote in this post:
Four Color Theorem 