Considering the smallest known non-Hamiltonian 3-regular planar graphs, discovered by Barnette-Bosák-Lederberg, I computed the Tait coloring and then deformed it to put in evidence the R-G cycles that in this case are four.

Links to the historical importance of this graph:

https://mathworld.wolfram.com/Barnette-Bosak-LederbergGraph.html

https://en.wikipedia.org/wiki/Barnette–Bosák–Lederberg graph

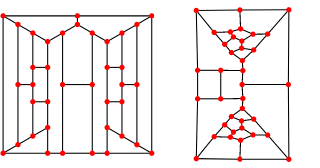
And here is the Tait coloring of this graph:

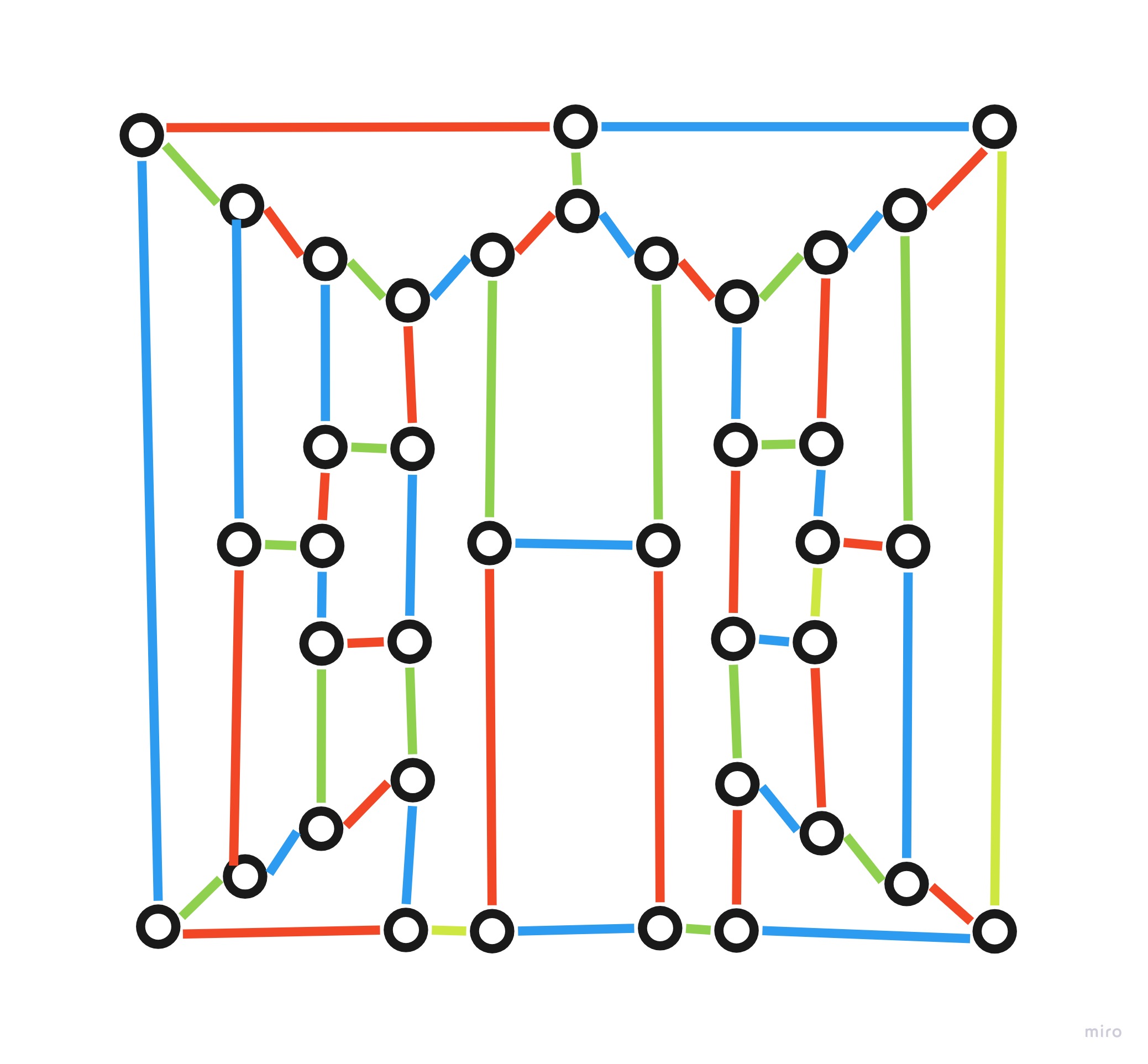
Deformed here to better show the R-G cycles: