Tag Archives: Kempe

Four color theorem: new ideas

Posted on by
1

This is what I want to try:

  • Select an F2, F3  or F4 preferably when it is near an F5 and remove the edge that joins the two faces
    • Analyse also the balance of the Euler’s identity when removing edges, to decide if it is better to choose other couple: F2 near the highest or other possibilities
  • Let Deepmind DQN (or Tensorflow) learn the best approach for selecting faces and remove the edges
    • Controls:
      • The selection of the face and the edge based on the characteristics of the neighbor faces
    • Scope:
      • Avoid the F5 worst case (in the rebuilding phase), when it is necessary to apply the random Kempe’s color switches to solve the impasse

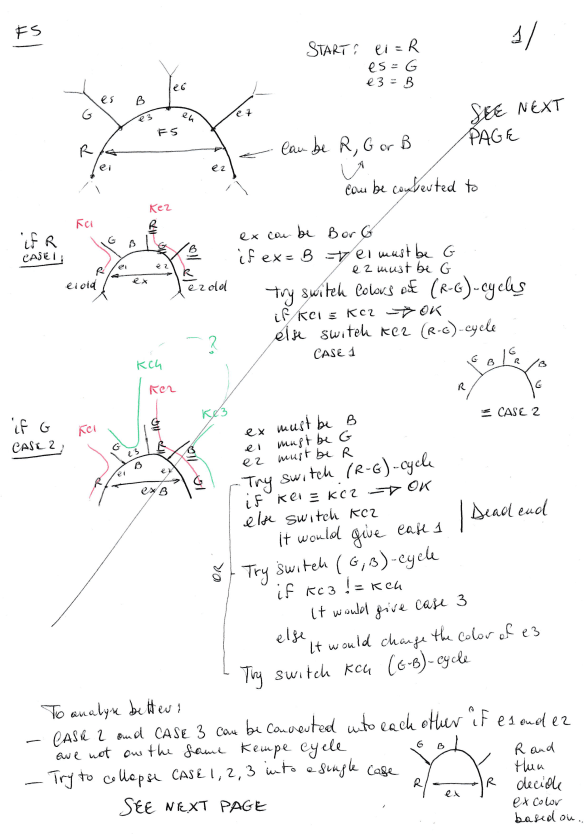
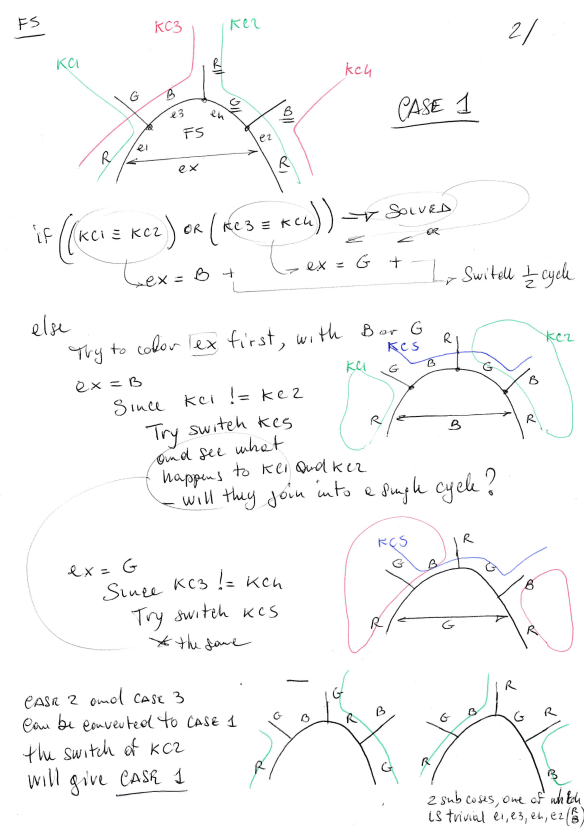
The rule: avoid F5 or at least do not create them.

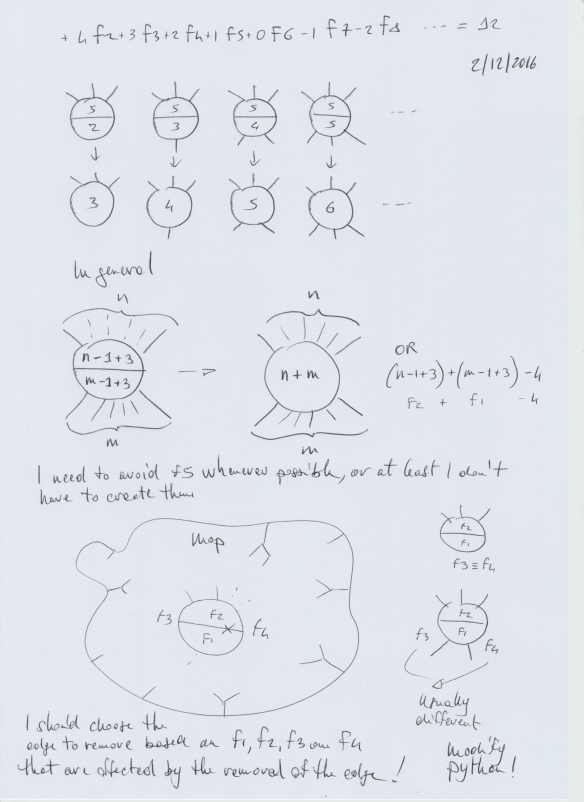
avoid-f5

  • Remove F2 when near F5 –> Good (will get rid of the F5 and generate an F3)
  • Remove F3 when near F5 –> Good (will get rid of the F5 and generate an F4)
  • Remove F4 when near F5 –> NOT Good (will end up with another F5)
  • Remove F5 when near F5 –> Good (will get rid of the F5 and generate an F6)

Other to avoid:

  • Remove F2 when near F7 –> NOT Good (will end up with another F5)
  • Remove F3 when near F6 –> NOT Good (will end up with another F5)
  • …

NOTE:

  • It is also important to check what appens to f3 and f4

Four color theorem: what next?

Posted on by
Reply

The algorithm I use to color graphs works pretty well … BUT:

  • Sometimes (very rarely) it gets into an infinite loop where also random Kempe color switches (around the entire graph) do NOT work. The good is, if I reprocess the same graph from the beginning (since in a part of the code I choose edges randomly), the algorithm usually works fine

So, what now?

I want to try other strategies while removing edges from the original graph, to avoid the above condition. I want to eliminate the need of random swithes.

The sequence I used so far is:

  • Select an F2 and if an F2 does not exist, select an F3 an so on: F4 and then F5. Once selected the face, I remove a random edge from it, only paying attention not to chose the edge if the resulting graph is 1-connected

I want to try:

  • Change the order of selecting the faces
    • Combinations
      • 2, 3, 4, 5 –> This is the default in the current version of the program (22/Nov/2016)
      • 3, 2, 4, 5
      • 4, 2, 3, 5
      • …
    • I want to try all possible combinations to see if … may be … if I’m really lucky, one does not require random swithes
  • Once selected the face, I want to try other strategies to select the edge to remove
    • random edge –> This is the default in the current version of the program (22/Nov/2016)
    • Among all the edges of the face, select the one that is shared with the face that has less edges respect to the other F
    • … that has more edges …

A planar cubic graphs to visualize what I wrote in this post:

haken-appel-hardest-case-map

Four color theorem: one switch is not enough :-(

Posted on by
Reply

Experimenting with the Python program, I have found that if you have an F5 impasse, a single switch may not be enough to solve the impasse. It means: counterexample found.

This is a bad news, since I believed that a single switch, on an appropriate edge, could have been the key to solve the theorem.

BUT

Since a limited number of switches still work, I am going to study if two switches, on appropriate edges, may work.

🙂

Four color theorem: down to a single case!

Posted on by
Reply

This post follows directly the previous one. I’m down to a single case to prove (pag. 3).

kempe-half-cycle-swapping-method-F5-third-page-v2

I think I should move to Java coding, implementing the entire algorithm: map reduction (removing edges), color reduced map, restore of edges one at a time, adjust the coloring to the case to prove (e2 = red), apply Kc5 color switching, …, apply the half Kempe-cycle color switching.

Notes (pag. 1 and 2):

kempe-half-cycle-swapping-method-F5-first-page

Second page:

kempe-half-cycle-swapping-method-F5-second-page