This page is dedicated to Cahit spiral chains. What I’m trying to do is to apply Cahit spiral chains to simplified rectangular maps and then add this tool to the java program I’m writing.
Disclaimer:
- These are just personal notes about spiral chains. Not being a mathematician, some of the content that I’ll insert here maybe initially wrong. Sorry for that. I’ll fix it if someone will let me notice the error!
Examples
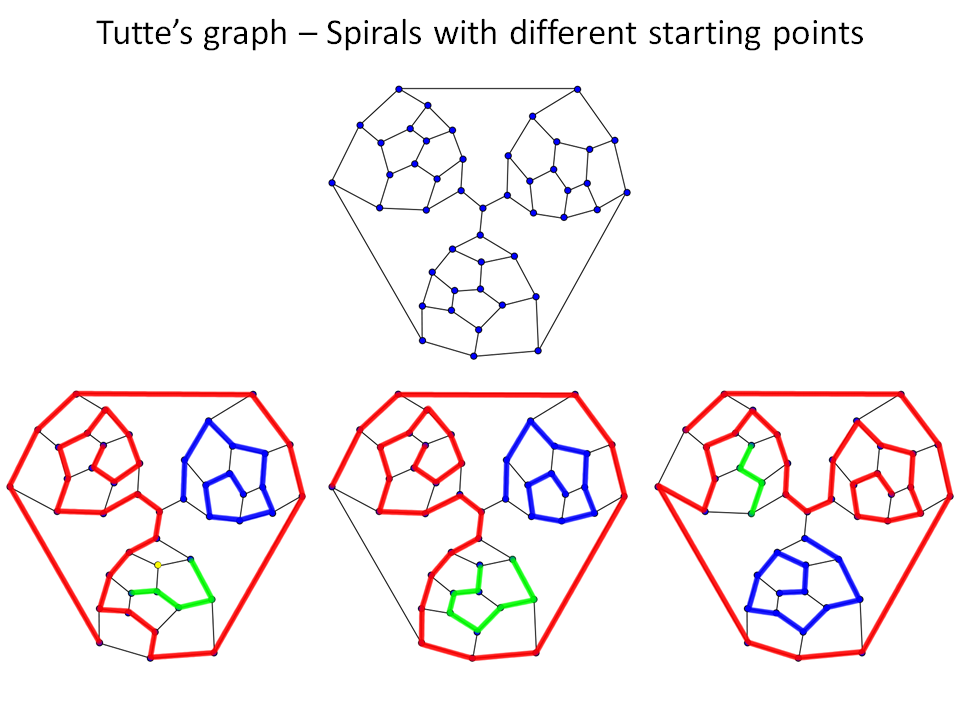
Example: Spiral chains change depending from the starting point. Considering that Tutte’s graph has a rotational simmetry of 120° (pinning the vertex at the center), only three different elaborations in spiral chains will be possible.
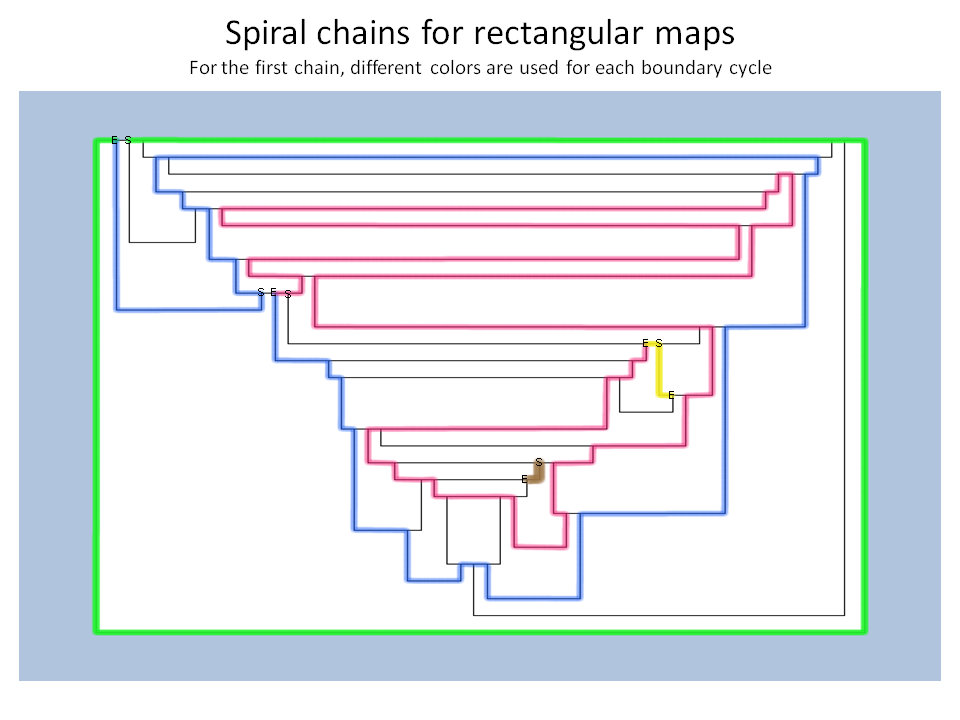
Example: This is the spiral chain elaboration for a rectangular map of 30 faces >= F5. If you need to recreate the map within the Java program, type in:
1b+, 20b+, 24b+, 29b+, 27b-, 28b-, 26b-, 24e-, 23b-, 25b-, 21b-, 22b-, 20e-, 17b-, 18b-, 21e-, 19b-, 16b-, 13b-, 7b-, 11b-, 12b-, 10b-, 4b-, 7e-, 9b-, 5b-, 4e-, 2b-, 3b-, 5e-, 6b-, 9e-, 10e-, 8b-, 6e-, 3e-, 11e-, 13e-, 14b-, 16e-, 17e-, 15b-, 14e-, 12e-, 18e-, 15e-, 8e-, 23e-, 22e-, 26e-, 27e-, 25e-, 19e-, 28e-, 29e+, 2e+, 1e+
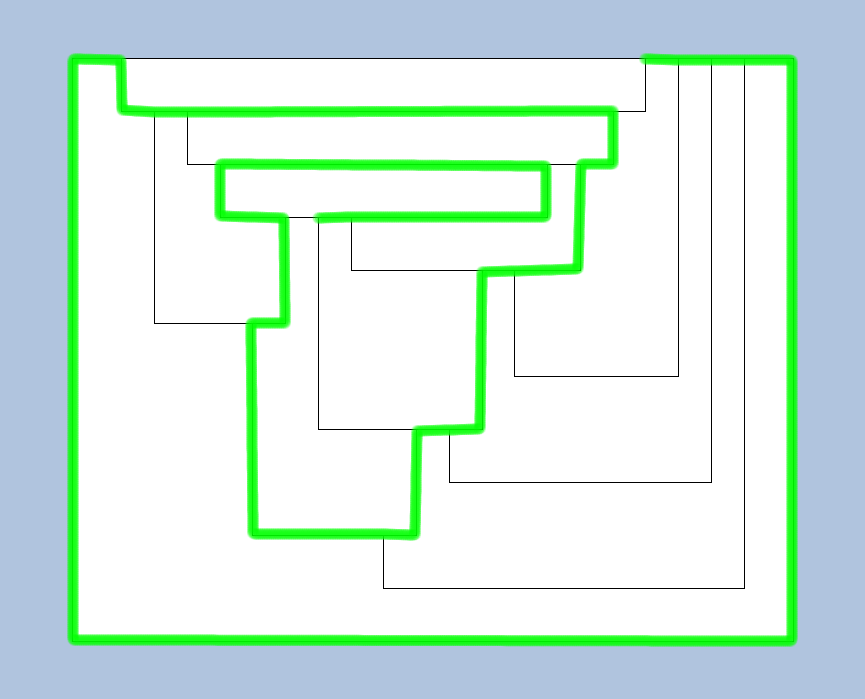
This is a rectangular map of 12 faces, that has only one spiral:
Notes on the algorithm: recognize the spiral chains
A very short way to express the spiraling algorithm is:
- Start from a vertex on the outer loop
- Go to the second vertex moving clockwise on the outer loop
- For all the other vertices of the spiral, always try to turn left
- If you can’t turn left (because you will end up on a vertex already visited), then turn right
- If you can’t turn right, it means the spiral terminates here
- …
Rules for the algorithm for the computer (clockwise spirals):
- Special rules
- The starting vertex of the first spiral chain has to be on the external cycle of the graph
- The starting vertex of all other spiral chains, if the previous spiral chain did not cover all vertexes, is the closest vertex to the last vertex of the previous spiral chain
- For the first move of the first spiral chain, walk on the edge of the external cycle moving clockwise
- Note: For the first move of the other spiral chains, the direction to choose is forced by the general rules, because one of the edges will surely reach a “used” vertex. This can be proved (but I think is not so trivial to prove) by the way the starting vertex of these spiral chains has been choosen
- General rules
- Every time you leave a vertex, mark it as “used” (not to be reached again), meaning also that you cannot walk on an edge that will take you on one of these “used” vertexes
- To identify the next vertex of the spiral chain, always choose the left-most edge. Remember also to apply the previous rules: if the left-most edge will take you to a vertex that has already be reached (consider also all previous spiral chains), use the other edge at the right
- Continue until all previous rules can be applied. The spiral chain ends when there is nothing else to do, and all rules will fail
Pseudocode:
spiral chain number = 1
all spiral chains found = false
number of all "used" vertices of the graph = 0
while (all spiral chains found == false) {
if (spiral chain number == 1)
move to a random vertex on the external cycle
}
else {
move to the closest unused vertex to the last vertex of the last spiral chain
}
spiral chain vertex number = 1
spiral chain completed = false
while (spiral chain completed == false) {
set the vertex as "used"
set all incident edges as "used"
if ((spiral chain number == 1) and (spiral chain vertex number == 1)) {
move to the second vertex of the external cycle clockwise
number of "used" vertices = number of "used" vertices + 1
}
else {
if (edge at left is not "used") {
move to the next vertex at the end of the left edge
number of all "used" vertices of the graph = number of all "used" vertices of the graph + 1
}
else if (edge at righ is "used") {
move to the next vertex at the end of the right edge
number of all "used" vertices of the graph = number of all "used" vertices of the graph + 1
}
else {
spiral chain completed = true
}
}
}
if (number of all "used" vertices of the graph == number of vertices of the graph) {
all spiral chains found = true
}
else {
spiral chain number = spiral chain number + 1
}
}
See the github project for the final implementation.
Notes on the algorithm: 3-edge coloring spiral chains (1 spiral chain)
To be finished.
Notes on the algorithm: 3-edge coloring spiral chains (n spiral chains)
To be finished.
Links to external pages, documents and other stuff
- If you consider to color the regions of a map by the spiral chain then see http://arxiv.org/abs/0903.4108
- If you consider to color the vertices of a maximal planar graph by the spiral chain see http://arxiv.org/abs/math/0408247 and http://arxiv.org/abs/0710.2066
- If you consider to color the edges of a bridgeless cubic planar graph (Tait’s coloring) by the spiral chain see http://arxiv.org/abs/math/0507127
- If you consider to repair Kempe-“proof” by the use of double-spiral chain see http://neu-tr.academia.edu/IbrahimCahit/Papers/1244468/The_Four-Color_Map_Theorem_Kempes_Fallacious_Proof_Repaired_ and first 6 pages of http://arxiv.org/abs/0903.4108