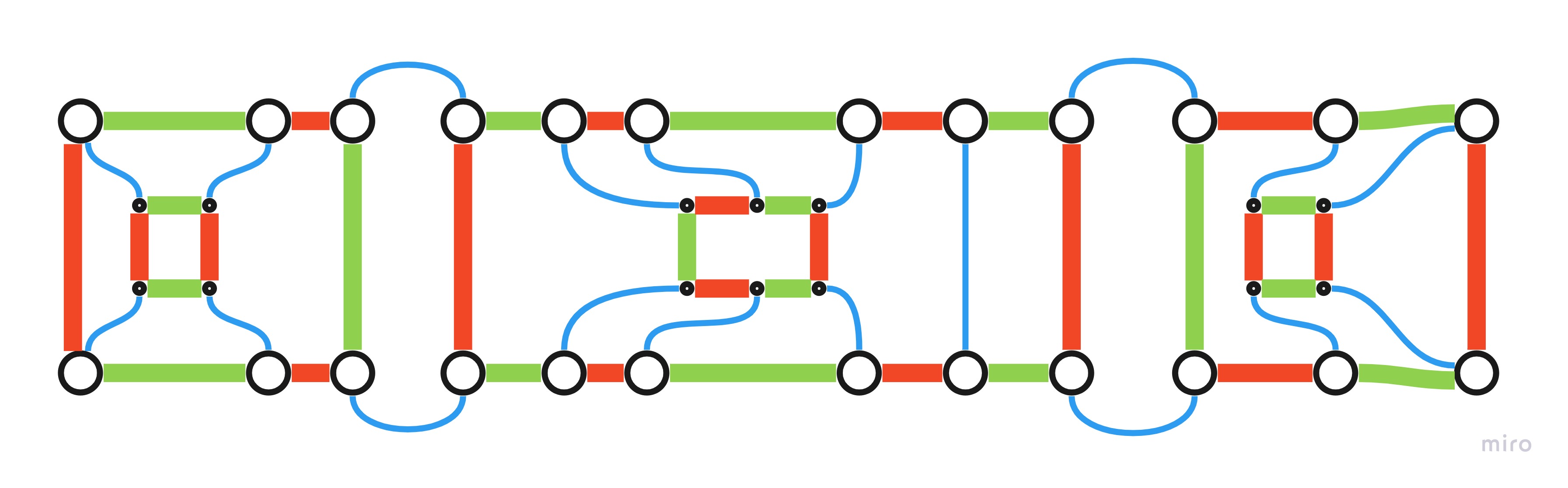
If you can prove that it is possible to decompose a 3-regular graph into cycles, all with even length, you have also proved the four color theorem.

I think this fact is already known, but I never paid too much attention to it before.

Naturally, also the opposite is true: since the 4CT is true, it means that it is possible to color it, and also get the Tait coloring. And for any two colors you choose (for example Red and Green), the related Kempe cycles form a partition of the graph and each cycle has an even number of edges.

Once the decomposition is found, since the cycles have an even number of edges, it is possible to color the edges of a cycle with two alternate colors (for example Red and Green), forming this way Kempe cycles. When all cycles are colored (with R and G), it is possible to use a third color (for example Blue) to color the remaining edges.

The resulting graph will have a Tait coloring for all edges, which is equivalent to coloring all faces with four different colors.

But, how difficult is it to find all cycles?

This one has 6 Red-Green cycles (all of even length), that form a division on the 3-regular planar graph into cycles.