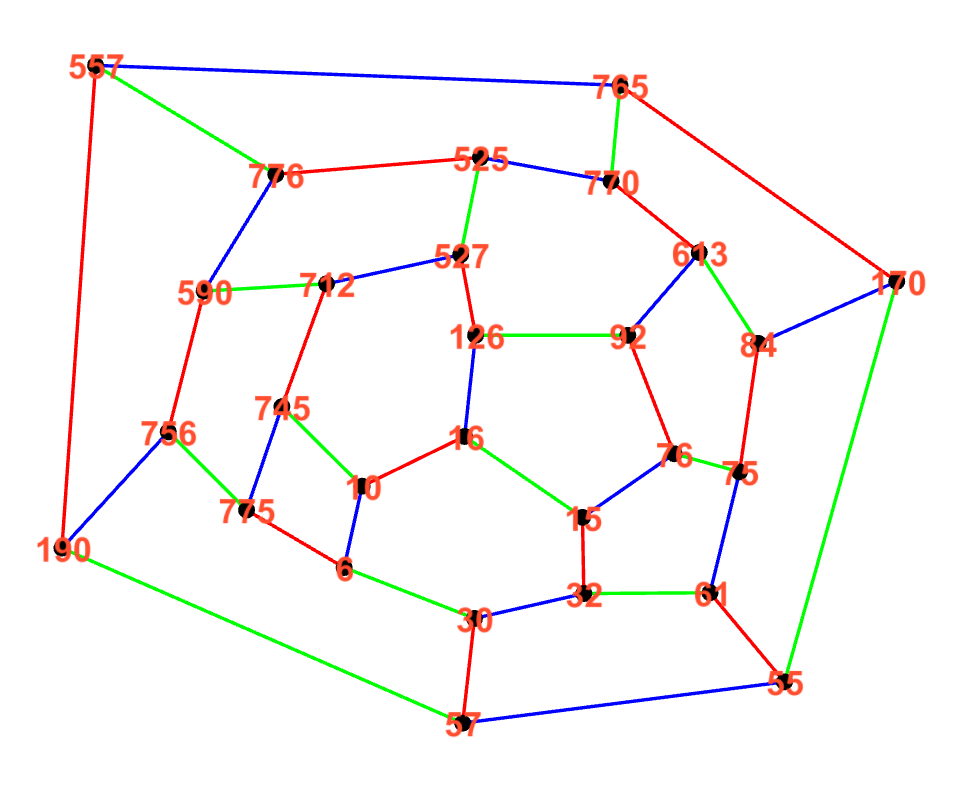
The other day, before going to sleep, I realized that I needed to revisit the problem, starting with a piece of evidence I had noticed long ago. When a map is colored, the corresponding Tait coloring of the borders creates color chains (R-G, R-B, or G-B) that always form loops. Moreover, there may be more than one loop for each pair of colors. For example, the map shown here has:

1 R-G loop

• 190, 557, 776, 525, 527, 126, 92, 76, 75, 84, 613, 770, 765, 170, 55, 61, 32, 15, 16, 10, 745, 712, 590, 756, 775, 6, 30, 57, 190

2 R-B loops

• 190, 557, 765, …, 756, 190
• 745, 712, 527, 126, 16, 10, 6, 775, 745

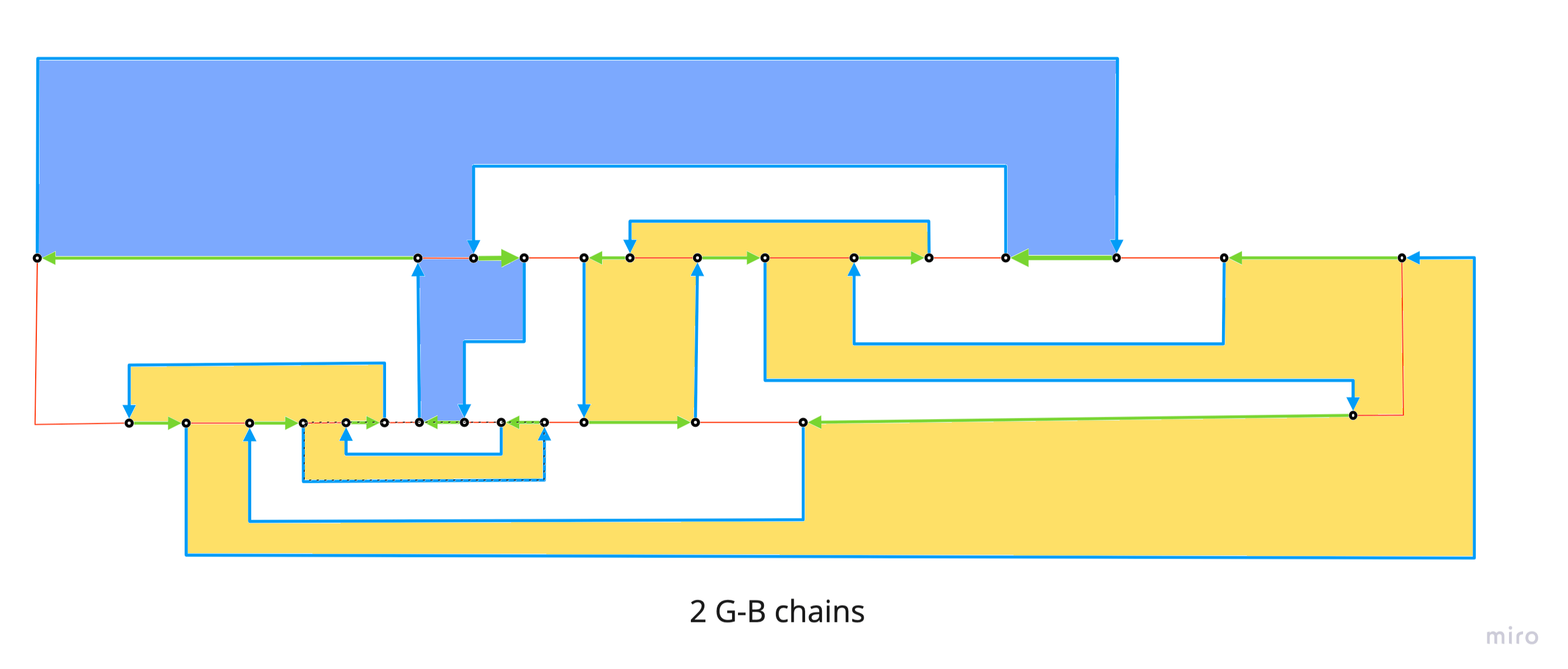
2 G-B loops

• 190, 57, 55, 170, …, 756, 190
• 776, 557, 765, 770, 525, 527, 712, 590, 776

I wonder if analyzing how these loops form during the rebuilding phase of a map, after the reduction phase (see other posts), can lead me out of the mud.

Notes:

• Once the map is completely four-colored (or 3-edge colored = Tait coloring), each chain (two-color chain) is actually a loop
  • This becomes clear when you consider the colors available at each vertex as you follow a chain. For example, if you’re examining the R-G chain and start from a vertex, following the Red color to the next vertex, that vertex will have the Green color available to continue the chain. As you keep alternating between R and G, each new vertex will offer the other color in the chain until you eventually return to the starting vertex, thereby closing the loop
• If only one chain for a specific color selection (R-G, R-B, or G-B) exists, that chain touches all vertices of the map
  • If it weren’t so, one of the vertices not on the chain still would have the edges colored with three different colors, two of which (the same two colors of the chosen chain) would form another chain
• The length of all loops is always an even number
  • This come straightforward from the definition of chain, multiple sequences of R and G = 2n

Deforming the original map, I managed to put in evidence the R-G loop, and then the other loops (R-B and G-B) respect to the first R-G deformation.

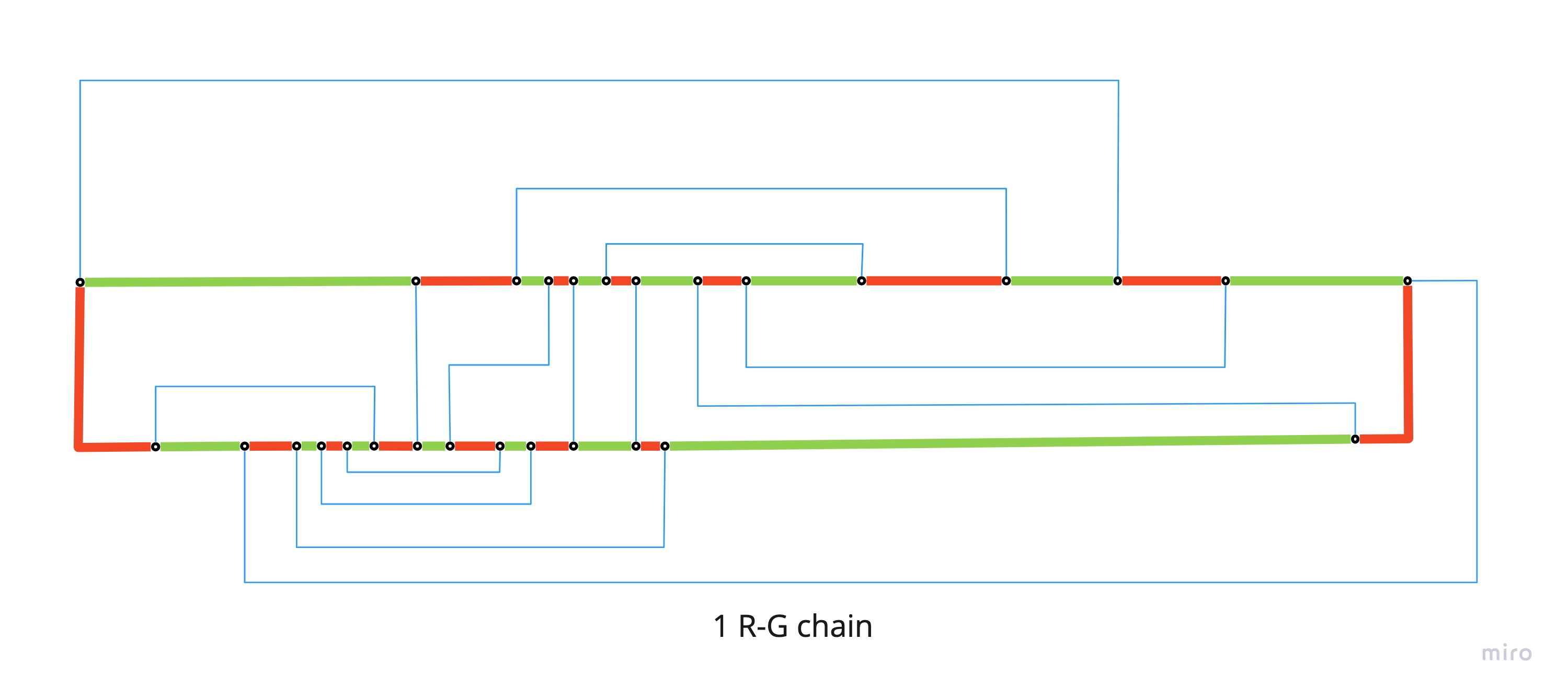
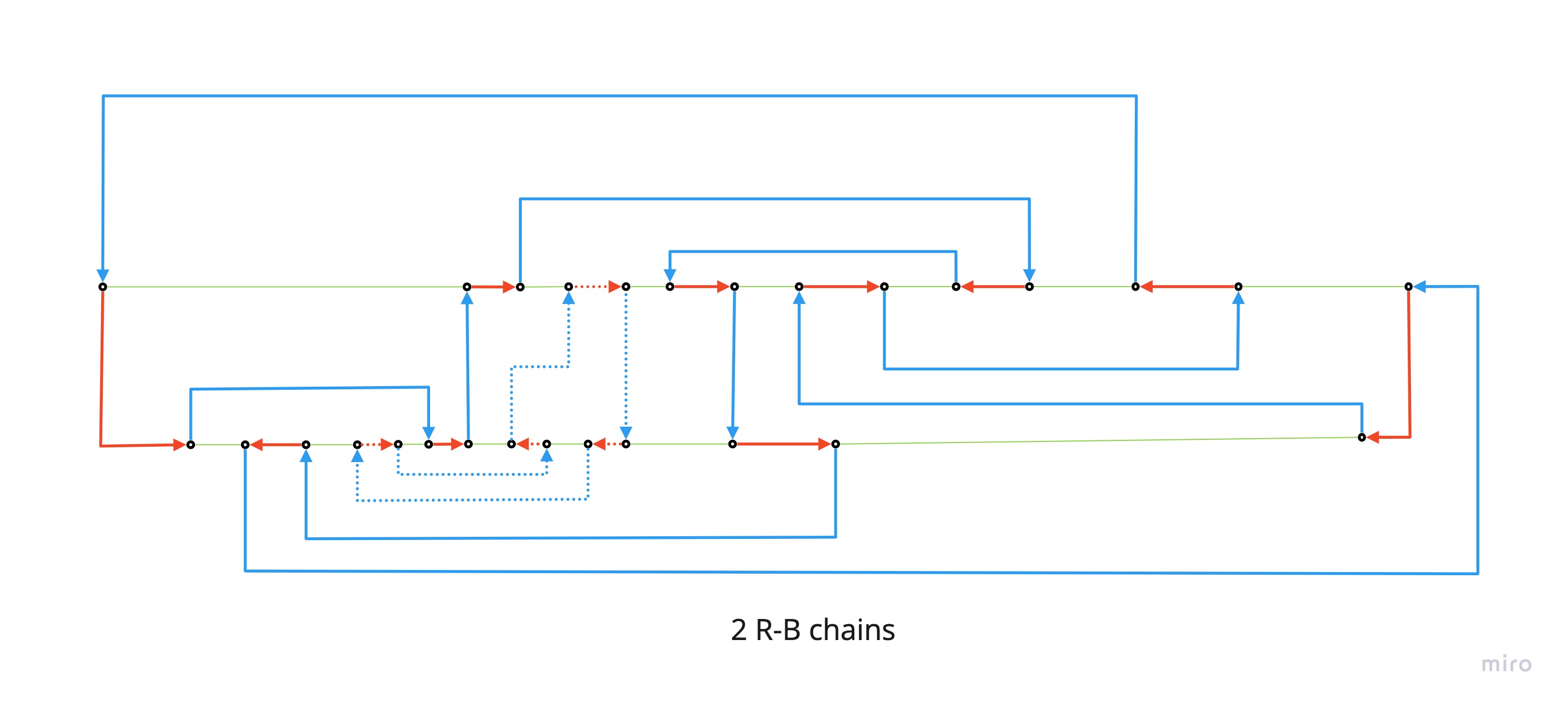
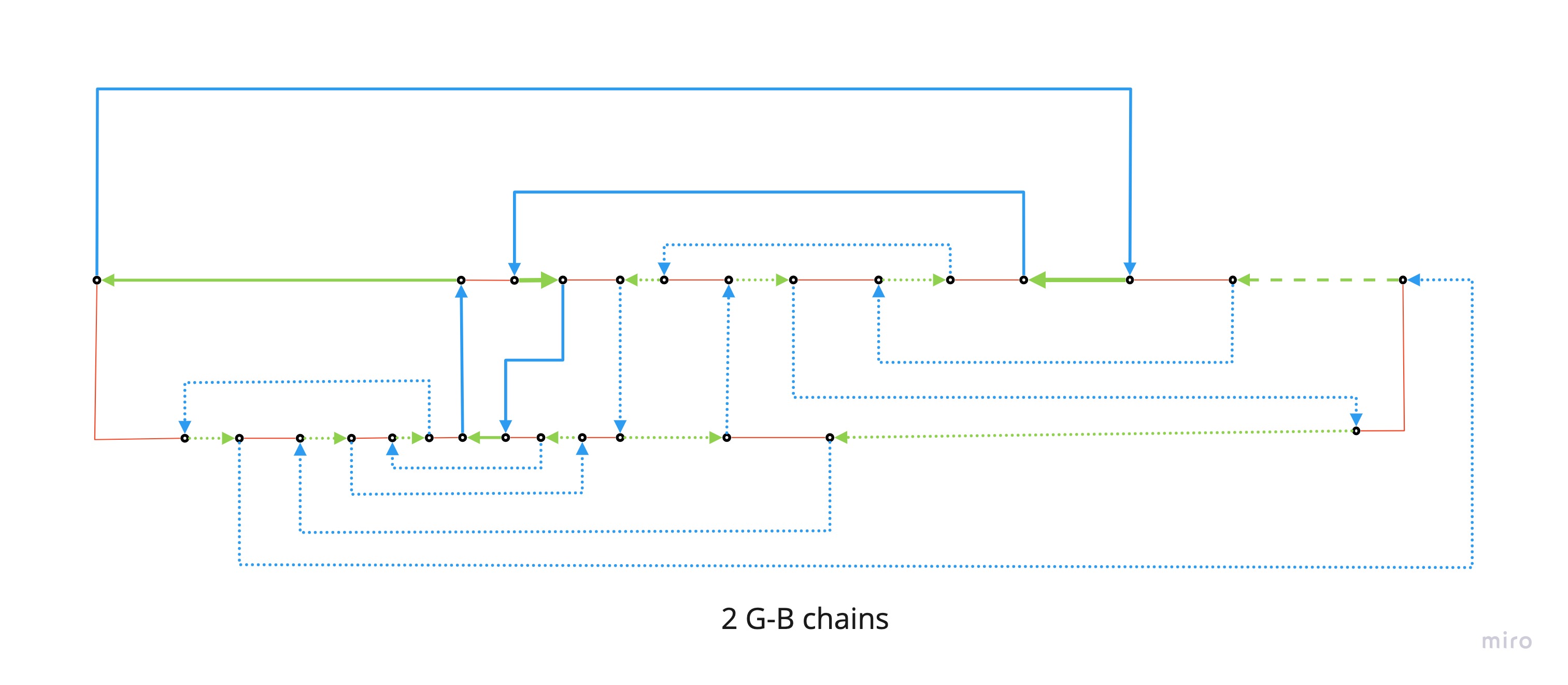
And here with the loops filled

Additional note:

This was the map when I discovered that infinite random switches throughout the entire graph do not solve the impasse. It was bad 😦 The graph here is identical to the one in the previous post.

https://four-color-theorem.org/2016/10/31/four-color-theorem-infinite-switches-are-not-enough/